Метрология и технические измерения отрасли: Программа, методические указания и контрольные задания, страница 4

где  – подозрительный результат,  – критерий Стьюдента при заданной доверительной вероятности и числе степеней свободы: . При этом оценки и  определяются без учета подозрительных результатов.

Если неравенство (6) выполняется, то подозрительный результат исключают (или заменяют средним значением если n мало).

Критерий «3σ» применяют, если количество измерений n ≥ 20…50. В соответствии с критерием считают, что результат с вероятностью 0,003 можно считать промахом если:

                                  (7)

Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, в пределах которого с заданной вероятностью находится истинное значение оцениваемого параметра.

Границы доверительного интервала определяют по формуле:

                                           (8)

Приведенные выше расчеты справедливы, если распределение полученных экспериментальных данных соответствуют нормальному. В соответствии с /2/ проверка нормальности распределения выполняется с помощью составного критерия.

Критерий 1. Определяем отношение  по формуле:

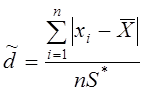                                             (9)

где S^* – смещенная оценка среднего квадратического отклонения, вычисляемая по формуле:

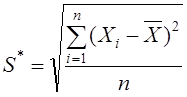                                      (10)

Результаты наблюдений группы можно считать распределенными нормально, если:

                                        (11)

где и  – квантили распределения, определяемые по табл. 2 по значениям n, q₁/2 и (1 – q₁/2), причем q₁ – заранее выбранный уровень значимости критерия.

Критерий 2. Можно считать, что результаты наблюдений принадлежат нормальному распределению, если не более m разностей превзошли значение z_P/2σ, где z_P/2 – верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности P/2. Значения P определяются из табл. 3 по выбранному уровню значимости q₂ и числу результатов наблюдений n.

В случае, если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.

После выполнения статистической обработки результат записывают в виде:

 (n =…, Р_Д=0,95)                       (12)

Таким образом, при статистической обработке группы результатов наблюдений в соответствии с /2/ следует выполнить следующие операции:

-  исключить известные систематические погрешности из результатов наблюдений;

-  проверить результаты на наличие грубых погрешностей и исключить их;

-  вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения;

-  вычислить оценку среднего квадратического отклонения результата наблюдения ;

-  вычислить оценку среднего квадратического отклонения результата измерения;

-  проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению;

-  вычислить доверительные границы случайной погрешности результата измерения;

-  вычислить доверительные границы погрешности результата измерения.

При вычислении доверительного интервала погрешности измерения необходимо учитывать следующее:

-  если < 0,8, то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата D =.

-  если  > 8, то случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что граница погрешности результата D = .

-  в случае, если неравенства не выполняются, границу погрешности результата измерения находят путем построения композиции распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины в соответствии. Допускается границы погрешности результата измерения D (без учета знака) вычислить по формуле:

D = KS_S,                                                   (13)

где K – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей; S_S – оценка суммарного среднего квадратического отклонения результата измерения.