Измерительные информационные системы (ИИС). Основные понятия. Назначение, классификация, структура, состав, функции, метрологические характеристики компонентов.
Цель задания – ознакомление с методами обработки экспериментальных данных, полученных в результате измерений с многократными наблюдениями.
Перед проведением измерений с многократными наблюдениями стараются исключить или максимально уменьшить систематическую погрешность, тогда погрешность результата измерений можно представить в виде суммы:
, (1)
где 
– неисключенная систематическая
погрешность, 
– случайная погрешность.
Неисключенная систематическая погрешность – составляющая погрешности результата измерений, обусловленная погрешностями вычисления и введения поправок на влияние систематических погрешностей или систематической погрешностью, поправка на действие которой не введена вследствие ее малости.
Кроме того, источником неисключенной систематической погрешности может быть погрешность применяемого средства измерений. Она постоянна для данного прибора, но в общем случае имеет случайное значение и указывается в нормативной документации в виде допустимого интервала. Определить систематическую погрешность прибора путем проведения повторных измерений одной и той же величины невозможно.
Случайной называют погрешность, изменяющуюся случайным образом (как по знаку, так и по величине) при повторных измерениях одной и той же физической величины. Случайная погрешность может быть обнаружена из-за разброса результатов измерений (или их погрешностей) относительно некоторого значения. Исключить полностью случайную погрешность нельзя, но ее можно существенно уменьшить, применив для обработки полученных результатов методы математической статистики. При проведении измерений с многократными наблюдениями стараются создать условия, при которых влияющие факторы действуют с одинаковой интенсивностью. (Влияющие факторы: несовершенство изготовления СИ, неточность их градуировки, изменение температуры и влажности окружающей среды, внешние электромагнитные поля, вибрации, субъективные ошибки человека-оператора и т. д., искажают результат). Полученную при этом погрешность называют ожидаемой.
В большинстве случаев случайная погрешность представляет собой случайную величину с нормальным законом распределения, основными числовыми характеристиками которого являются математическое ожидание М[X] и дисперсия D[X]:
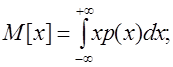(1)
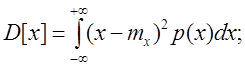(2)
Так как количество измерений – конечная величина, не превышающая 20÷50, а также, чтобы обеспечить одинаковую размерность характеристик случайной погрешности, в метрологии используют оценку математического ожидания – среднее арифметическое значение:
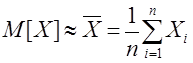(3)
и оценку среднего квадратического отклонения – (СКО):
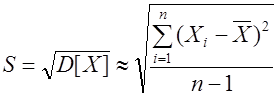(4)
где Хi – результат i – го измерения, n – количество наблюдений.
Полученные оценки являются случайными величинами, т.к. при проведении повторных измерений будут получаться иные значения. Поэтому часто используют оценку СКО среднего арифметического, определяемую по формуле:
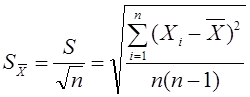(5)
Однако в ходе выполнения измерений могут быть получены результаты, погрешность которых значительно отличается от ожидаемой. Такие погрешности называют грубыми или промахами, и они должны быть исключены из массива обрабатываемых данных. Для определения грубых погрешностей используют статистические критерии: Романовского, «3σ» и другие.
В соответствии с критерием Романовского, который применяется, если число измерений меньше 20, подозрительный результат считается грубой погрешностью или промахом, если выполняется неравенство:
(6)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.