Оптика: основні формули і приклади розв’язування задач

5  ОПТИКА

Основні формули

Абсолютний показник заломлення 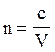 , де с - швидкість світла у вакуумі; V – швидкість світла у середовищі.

          Відносний показник заломлення другого середовища відносно першого n₂₁ = n₂/n₁ =V₁/V₂, де n₁  та  n₂ – абсолютні показники заломлення  співвідносно першого і другого середовищ;  V₁ та  V₂   - швидкості світла в середовищах.                                                                     

Оптична різниця шляху двох світлових хвиль

D = L₁ - L₂,

де  L - оптична довжина шляху світлової хвилі, що дорівнює

L = n,

де   - геометрична довжина шляху світлової хвилі в середовищі з показником заломлення n.

Залежність різниці фаз  Dj від оптичної різниці шляху світлових хвиль

Dj =D,

де  l - довжина світлової хвилі.

Умови максимального посилення світла при інтерференції

D = ± ml

і максимального послаблення світла

D ± (2m + 1),             де m = 0, 1, 2 ...

Оптична різниця шляху світлових хвиль, що утворюється при відбиванні монохроматичного світла від тонкої плівки,

D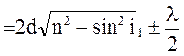

або

D,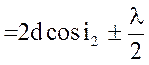

де  d - товщина плівки; n - показник заломлення плівки;  і₁ - кут падіння; і₂ - кут заломлення світла в плівці. Знак «плюс» вживається, коли показник заломлення плівки n менше, ніж показник середовища, «мінус» - коли більше.

Радіус світлих кілець Ньютона у відбитому світлі

,          (m = 1, 2, 3,...)

де m - номер кільця;  R - радіус кривини лінзи.

Радіус темних кілець Ньютона у відбитому світлі

.

При дифракції світла від однієї щілини умови спостереження максимумів

а,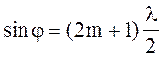

а мінімумів                                 а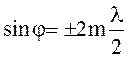,          (m = 0, 1, 2, 3, ...)

де  а  - ширина щілини;  m - порядковий номер максимумів і мінімумів; j - кут дифракції.

При дифракції світла від дифракційної гратки умови спостереження максимумів  

d sinj = ml,

де d - період дифракційної гратки.

Розділювальна здатність дифракційної гратки

R = l/Dl = kN,

де D l - найменша різниця довжин хвиль двох сусідніх спектральних ліній (l  та     l + Dl), при котрій ці лінії виглядають розділеними;  N - повне число щілин гратки;  k - порядок спектру.

     Формула Вульфа-Брегов

2d sinJ = ml,

де  J - кут ковзання (кут між напрямком рентгенівських променів та атомною площиною кристалу);   d - відстань між атомними площинами кристалу.

       Закон Брюстера 

tgi_Б =  n_21,

де  i_Б - кут Брюстера, тобто кут падіння , при якому відбитий від діелектрика промінь повністю поляризований в площині, перпендикулярній площині падіння, якщо за площину поляризації вважати площину коливань вектора електричної напруженості .

Закон Малюса

І = І_оcos²a,              або            І = ½ І_пр . cos²a,

де І_о - інтенсивність плоскополяризованого світла, що пройшло через поляризатор; І - інтенсивність цього світла після аналізатора; a - кут між напрямом коливань електричного вектора світла, що падає на аналізатор, та оптичною віссю аналізатора; І_пр - інтенсивність природнього світла, що падає на поляризатор.

Якщо у поляроїда частина інтенсивності світлового пучка поглинається і коефіцієнт поглиняння дорівнює k, тоді закон Малюса виглядає

І = І_о (1 - k)² cos²a

або

І =  ½ І_пр (1 - k)² cos²a

Кут повороту площини поляризації монохроматичного світла при проходженні крізь оптично активне середовище:

а) j = ad      ( у твердих тілах ),

де a - стала повертання;  d - довжина шляху світла у оптично активному середовищі;

б) j = a_рСd          (у розчинах),

де  a_р - питоме повертання; С - масова концентрация оптично активної речовини у розчині.

Закон Стефана-Больцмана        R = sT⁴,

де R - енергетична інтегральна світність абсолютно чорного тіла;

s - стала Стефана - Больцмана; Т - термодинамічна температура.

 Закон зміщення Віна

l_m = b/Т,

де l_m -  довжина хвилі, на яку припадає максимум спектральної світності; b –стала Віна.

  Другий закон Віна. Максимальна спектральна світність абсолютно чорного тіла

r(l, Т) _max =СT⁵, де  r (l, T)_max;   С - стала.

Енергія фотона e = hn,

де h  - стала Планка;  n - частота фотона.

   Маса фотона

m = e/c²  ,

де l - довжина хвилі фотона.

    Імпульс фотона

Р = mc .

        Формула Ейнштейна для фотоефекту

h n = A + T = A +,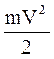

де  hn  - енергія фотона, що падає на поверхню металу; А  - робота виходу електрона; Т -  кінетична енергія фотоелектрона.

Червона границя фотоефекту    =   або   ,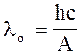

де  n_о - мінімальна частота світла, при якій ще відбувається фотоефект;  l_о - максимальна довжина хвилі, що дорівнює l_о  = с/n_о;  h  - стала Планка.

Формула Комптона

Dl = l ₂- l₁ =

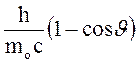
або

Dl =   l₂   -  l ₁ = ,

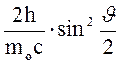де  l₁ - довжина хвилі фотона, що зустрівся з вільним чи слабовзв’язаним електроном ;  l₂ - довжина хвилі фотона, розсіяного на кут J після зіткнення з електроном; m_o - маса спокою електрона.

Комптоновська довжина хвилі

l_к =  h/m_oc; l_k = 2,436 пм.

Тиск світла при нормальному падінні на поверхню

Р = Е_е ( 1 + r)/с = w (1 + r),

    де Е_е - енергетична освітленість чи густина потоку енергії; w - об’ємна густина енергії, що падає на поверхню;  r - коефіцієнт відбивання . Ф_е - поток енергії Е

Ф_е = Е/t,  E_e = Ф_е/S = E/(t  . S),

де t – час;  S - площа поверхні.

Приклади розв’язування задач

                   Приклад 1 . На скляний клин з малим кутом a вертикально падає паралельний пучок променів монохроматичного світла з довжиною хвилі l = 0,6 мкм. Число k виникаючих при цьому інтерференційних смуг, що припадають на відрізок клина довжиною = 10^-2 м, дорівнює 10. Знайти кут  a клина.

Розв’язання

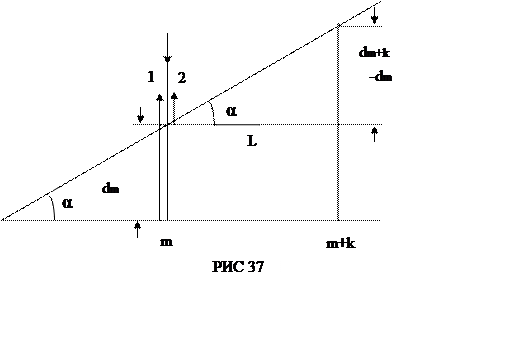
 Паралельний пучок світла відбивається від верхньої та нижньої граней. Ці пучки когерентні і тому на поверхні клину утворюються інтерференційні смуги. Вважаємо, що відбиті пучки 1 та 2 (рис.37) паралельні, тому що кут a малий. Різниця ходу променів 1 та 2 може бути визначена за формулою для інтерференції на тонкій плівці при умові нормального падіння променів, тобто                                    D = 2d_mn cos i₂ -.                              (1)

     Якщо різниця ходу D дорівнює непарному числу половин довжин хвиль, то утвориться темна інтерференційна смуга.

2d_m n cos i₂ -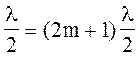-,                     (2)

тут d_m - товщина  клину у тому місці, де утвориться темна смуга з номером «m»; і₂ - кут заломлення , що дорівнює нулю. Після спрощень одержимо

2d _mn = ( m + 1)l                                   (3)

Якщо темній смузі номера  ( m +к) відповідає товщина клину  d_m+к ,то, врахувавши, що k смуг утворюється на відстані  l, з малюнка знайдемо

sin a = (d_m+к - d_m))/l,                               (4)

d_m+к можна знайти з рівняння (3) після підстановки ( m + k) замість m:

2d_m+к . n = (m + k + 1)l                      (5)

Підставим d_m  та  d_m+к у рівняння (4) та, врахувавши, що sin a = a ( a<5°), знайдемо

a =[(m + k+1)l - (m + 1 )l]/(2nl) = kl/(2nl)

Після підстановки фізичних величин знайдемо

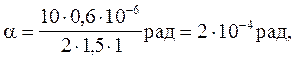
у секундах  дорівнює

a = 2 . 10^-4 .2,06 . 10^5¢¢ = = 41,2¢¢,

тому, що 1 рад » 2,06 . 10⁵¢¢.

          Приклад 2. На дифракційну гратку нормально до її поверхні падає монохроматичне світло. Період гратки  d = 2 мкм. Знайти найбільший порядок дифракційного максимуму, що дає ця гратка для червоного світла ( l = 0,7 мкм)

Розв’язання.

            З умови головного дифракційного максимуму дифракційної гратки знайдемо порядок максимуму

 m = ( d sin j)/ l,

де  d  - період гратки; j - кут дифракції;  l - довжина хвилі монохроматичного світла.                                                                                                                             Число m  не може бути більше ніж  d/l, тому що sin j £ 1, тобто m £ d/l

Після підрахування отримаємо  m £ 2 /0,7 = 2,86 , тобто   m_max = 2, тому що порядок максимуму є ціле число.