Фізичні основи класичної механіки: основні формули і приклади розв’язування задач

1 ФІЗИЧНІ ОСНОВИ КЛАСИЧНОЇ МЕХАНІКИ  

Основні формули

Кінематичне рівняння руху матеріальної точки (центра мас твердого тіла) вздовж осі  х

х = ¦(t),

де  ¦(t)  є деяка функція часу

    Проекція миттєвої швидкості на вісь  х

V_x =  dx / dt

    Проекція середньої швидкості на вісь   х

<V_x> =  D x / D t

  Проекція миттєвого прискорення на вісь   х

а_х  = dV_x  / dt

  Проекція  середнього прискорення на вісь  х

< a_x> =   D  V_x /  D t

  Кінематичне рівняння руху матеріальної точки по колу

j=¦(t) при    r  =  R = const

 Модуль кутової швидкості

w=dj/dt

 Модуль кутового прискоренняя

e  = dw / dt

    Зв’язок між модулями лінійних та кутових величин, які характеризують рух точки по колу.

V = wR,     a_t  = eR,    a _n = w²R,

де V - модуль лінійної швидкості;

а_t - модуль тангенціального прискорення;

а_n - модуль нормального прискорення.

Імпульс матеріальної точки масою m, яка рухається зі швидкістю  V, дорівнює

р= mV

Другий закон Ньютона,

dр/dt = F,

де  F -  результуюча сила.

Сили, які розглядаються в механіці

а) сила пружності

F = - kx,

де k  - коефіцієнт пружності;

х  - абсолютна деформація;

б) сила тяжіння

P = mg ;

в) сила гравітаційної взаємодії

F = G  (m₁ m₂ )/ r²,

де  G  - гравітаційна стала;

m₁, m₂ - маси взаємодіючих тіл;

r  - відстань між ними.

г) сила тертя (ковзання)

F = f  N,

де   f -  коефіцієнт тертя;

       N - сила нормального тиску.

          Закон збереження імпульсу

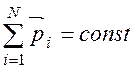
або для двох тіл ( і = 2)

,

де  V₁  i V₂ - швидкості тіл в початковий момент часу;

U₁  та  U₂ -  швидкості тих же тіл в кінцевий момент часу.

Кінетична енергія тіла, яке рухається поступово,

Т = mV² / 2

або

T = p² / 2m

Потенціальна енергія

а) пружнодеформованої пружини

П  = 1/2  KX²,

де  К  - коефіцієнт пружності;

Х  - абсолютна деформація;

б) гравітаційної взаємодії

П = - G  (m₁ m₂) / r,

де  G - гравітаційна стала;

     m₁  та m₂ - маси взаємодіючих тіл;

          r - відстань між ними;

          в) тіла, яке знаходиться в однорідному полі сили тяжіння Землі,

П = mgh,

де  g  - прискорення вільного падіння;

     h - висота тіла над рівнем, прийнятим за нульовий ( формула вірна при умові, що h << R - радіуса Землі.)

Закон збереження механічної енергії

Е = Т + П = соnst

Робота  А, звершена результуючою силою, визначається як міра змінювання кінетичної енергії матеріальної точки

А=D Т = Т₂ - Т₁

Основне рівняння динаміки обертального руху відносно нерухомої осі  Z.

M_{z =}  I_z . e,

де  M_z - результуючий момент зовнішніх сил, які діють на тіло, відносно осі  Z;

  e - кутове прискорення;

  I_z - момент інерції відносно осі обертання.

        Момент інерції деяких тіл масою  m відносно осі Z, яка проходить через центр маси:

     а) стержня довжиною  l відносно осі, яка перпендикулярна стержню,

I =ml² ;

        б) обруча ( тонкостінного циліндра) відносно осі, перпендикулярної площині обруча (вісь  Z співпадає з віссю циліндра),

I_z= mR²,

де  R - радіус обруча (циліндра);

   в) диску радіусом  R відносно осі, перпендикулярної площині диску

I _z= mR².

Проекція на вісь Z моменту імпульсу тіла  L_z, що обертається відносно нерухомої осі Z,

L_z = I_z . w_z,

де  w_z - кутова швидкість тіла.

Закон збереження моменту імпульсу системи тіл відносно осі  Z

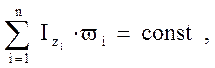
де  w_i -кутова швидкість обертання системи тіл навколо осі  Z.

          Кінетична енергія тіла, яке обертається навколо осі   Z,

Т = 1/2 (I_z . v²_z)      або             T = L²_z / (2 I_z)

Релятивістська маса

m =,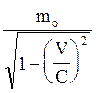

де   m_o -  маса спокою;  V - швидкість частинки; с - швидкість світла; причому повинна виконуватись умова  V » c.

          Релятивістський імпульс

р = mV =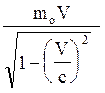

Енергія релятивістської частинки

Е = mc² = m_oc²  + Е_k,

де Е_к  - кінетична енергія частинки;  m_oc² = E_o - її енергія спокою.

Зв’язок повної енергії з імпульсом релятивістської частинки

Е² - р²с² =  m²_oc⁴

Зв’язок кінетичної енергії з імпульсом   релятивістської частинки

p =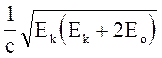

Приклади розв¢язування задач

Приклад 1. Рівняння руху матеріальної точки вздовж осі х має вигляд

x = A + Bt + Ct³,

де      А = 2 м

          В = 1 м/с

          С = -0,5 м/c²

          Знайти координату Х, швидкість  V_x та прискорення  а_х точки в момент часу  t = 2 c.

          Розв’язання. Координату Х визначимо, якщо підставимо в рівняння руху числові значення коефіцієнтів А, В, С та часу t;

Х = (2 + 1 . 2 - 0,5 . 2³) м = 0

Миттєва швидкість відносно осі Х є перша похідна від координати по часу

V_x = dx/dt = B + 3Сt²

Прискорення точки визначимо, якщо знайдемо похідну від швидкості по часу

а_х = dV_x/dt = 6Сt

В момент часу  t = 2с

V_x = (1 - 3 . 0,5 . 2²) м/с = -5 м/с

а_х = 6 (-0,5) . 2 м/с² = -6 м/с²

 

Приклад 2. Тіло обертається навколо нерухомої осі за законом

j = A + Bt + Ct²,

де      А = 10 рад,

          В = 20 рад/с,

          С = -2 рад/c².

Визначити повне прискорення aточки, яка знаходиться на відстані r = 0,1 м від осі обертання, для моменту часу  t = 4 с.

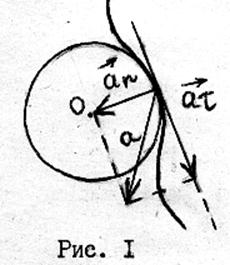Розв’язання. Повне прискорення a точки, що рухається по кривій лінії, можна визначити, як геометричну суму тангенціального прискорення a_t,  направленого по дотичній  до траєкторії, та нормального прискорення а_n, що направлене до

 центру кривини траєкторії (рис.1)     

    взаємно перпендикулярні і тому модуль прискорення дорівнює

a 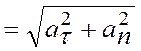                   (1)

Модулі тангенціального та нормального прискорень точок тіла, що обертається, можно визначити за формулами

a_t=  er,     a _n = w²r,

 де   w - модуль кутової швидкості тіла,

 e-  модуль його кутового прискорення.

        Для повного прискорення  = будемо мати  вираз

   (2)

Кутову швидкість  w визначимо, якщо візьмемо першу похідну від кута повороту по часу

w=dj/dt = B+2Ct

В момент t = 4 c модуль кутової швидкості

w = 20 +( 2 - 2.4) рад/с = 4 рад/с.

Кутове прискорення знайдемо, якщо візьмемо першу похідну від кутової швидкості по часу

                                                     e= dw/dt = 2C = -4 рад/с²

Підставимо значення v, e  та  r у формулу (2) , будемо мати

a  = 0,1      

 

      Приклад 3. Через блок в вигляді суцільного диску, що має масу  m= 80 г,

перекинута тонка гнучка нитка, до кінців якої підвішені тягарці масою  m₁ = 100г та m₂= 200 г (див.рис.2). Визначити прискорення, з яким будуть рухатися тягарці. Тертям та масою нитки знехтувати.