162. На краю платформи у вигляді диску радіусом R=3 м стоїть людина масою m= 70 кг. Платформа обертається навколо вертикальної осі з частотою n1 = 8 хв -1. Коли людина перейшла в центр платформи, платформа стала обертатись з частотою n2 = 10 хв-1. Визначити масу платформи. (Момент інерції людини обчислювати як матеріальної точки).
163. Яка частота і кутова швидкість обертання колеса вітродвигуна, якщо за 2 хв. колесо зробило 50 обертів?
164. Стержень довжиною l = 1 м обертається навколо осі, яка проходить через центр ваги, з кутовою швидкістю w1 = 0,5 с-1. На один з кінців стержня з гори падає пластилінова кулька і прилипає до нього. Маса кульки m2 = 30 г. З якою швидкістю почне обертатись стержень? Кульку вважати матеріальною точкою, маса стержня m1 = 0,3 кг.
165. Горизонтальна платформа масою m = 80 кг і радіусом R= 1 м обертається з частотою n1 = 20 об/хв. В центрі платформи стоїть людина і тримає в розставлених руках гирі. З якою частотою n2 буде обертатися платформа, якщо людина опустить руки, зменшивши свій момент інерції з I1 = 2,94 до I2 = 0,98 кг . м2? Платформу вважати однорідним диском.
166. Горизонтальна платформа масою m = 100 кг і радіусом R = 1 м обертається з частотою n1 = 20 об / хв. В центрі платформи стоїть людина і тримає горизонтально стержень довжиною 2 м і масою m2= 6 кг. З якою частотою почне обертатись платформа, якщо людина поставить стержень вертикально в центрі платформи?
167. Фігурист з розставленими руками обертається зі швидкістю w1 = 2 об/с, при цьому його момент інерції дорівнює I1 = 2,94 кг . м2. З якою швидкістю він стане обертатись, якщо різко зігне руки, тим самим зменшуючи момент інерції до I2 = 0,98 кг . м2?
168. Однорідний диск масою m радіусом R може вільно обертатись навколо осі, яка проходить через центр диску перпендикулярно його площині. Куля масою m, яка має швидкість V1, влучила в диск і застряла в ньому. Знайти кутову швидкість обертання диску разом з кулею (див.рис.4).
|
|||
|
|||
|
|
169.
Як зміниться кутова швидкість обертання планети, якщо на її поверхню впаде
метеорит масою m, який летів в площини екватора планети зі
швидкістю V?
РИС 4
Маса планети М,
і її радіус R відомі (див.рис.4).
|
|
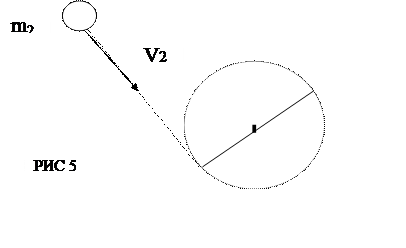170. Стержень довжиною l = 1 м обертається навколо осі, яка проходить через центр ваги, з
кутовою швидкістю w = 0,5 с-1. В
один з кінців стержня влучає пластилінова кулька і прилипає до нього. З якою
кутовою швидкістю w2 почне обертатись стержень? Маса стержня m1 = 0,3 кг,
маса кульки m2
= 30 г., швидкість її V2 = 2 м/с. При
розрахунках кульку вважати матеріальною точкою (див.рис.5)
171.Диск масою m = 2 кг котиться без ковзання по горизонтальній площині зі швидкістю V = 4 м/с. Знайти кінетичну енергію Т диску.
172. Мідна куля радіусом R=10 см обертається з частотою n = 2 об/с навколо осі, яка проходить через центр. Яку роботу треба виконати, щоб збільшити кутову швидкість обертання кулі вдвоє?
173. Визначити лінійну швидкість центра кулі, яка скотилась без ковзання з похилої площини висотою h = 10 см
174. Куля масою m = 10 г летить з швидкістю V= 800 м/с, обертаючись навколо повздовжньої осі зі частотою n = 3 . 103с-1. Вважаючи кулю за циліндрик діаметром d = 8 мм, визначити повну кінетичну енергію кулі.
175. Дві пружні кулі, маса яких m1 = 10 кг і m2 = 15 кг, рухаються назустріч одна одній зі швидкостями V1 = 6,0 м/с і V2 =3,0 м/с. Які швидкості вони матимуть після зіткнення ?
176. По похилому помосту завдовжки l = 8 м і заввишки h=1,6 м піднімають вантаж, маса якого 225 кг. Коефіцієнт тертя дорівнює ¦ = 0,1. Визначити корисну та повну роботу і коефіцієнт корисної дії.
177. З якою швидкістю треба кинути м'яч униз, щоб він підскочив на 5 м вище того рівня, з якого його було кинуто ? Удар об Землю вважати пружним.
178. Тіло масою m = 1,5 кг, яке було кинуто вертикально догори з висоти h = 4,9 м зі швидкістю V1 = 6 м/с, впало на землю зі швидкістю V2 = 5 м/с. Визначити роботу сили опору повітря.
179. Дві пружні кулі,маса яких m1= 18 кг і m2 = 12 кг, рухаються назустріч одна одній, причому швидкість першої кулі становить V1 = 8,0 м/с. Після удару перша куля зупинилась, обчислити швидкість другої кулі до удару та після . Зіткнення вважати центральним і пружним.
180. Пружна куля, маса якої m1= 30 г, рухалася зі швидкістю V2 = 20 см/с і наздогнала другу пружну кулю, що мала масу m2 = 50 г і швидкість V2 = 12 cм /с. Визначити швидкість куль після удару (удар пружний, центральний).
181. Яку частку швидкості світла має швидкість частинки, щоб її кінетична енергія була рівною її енергії спокою ?
182. На скільки збільшиться маса a - частинки при прискоренні її від початкової швидкості, рівної 0, до 0,9 швидкості світла?
183. Сінхрофазотрон дає пучок протонів з кінетичною енергією в 10 ГеВ. Яку частку швидкості світла складає швидкість протонів в цьому пучку?
184. Електрон пройшов прискорюючу різницю потенціалів 108 В. В скільки разів змінилась маса електрона? Чому дорівнює швидкість електрона ?
185. Швидкість руху тіла рівна 0,6 с. На скільки відсотків зросла густина тіла?
186. Визначити релятивістський імпульс протона, якщо швидкість його руху 0,8 С.
187. Визначити швидкість, при якій релятивістський імпульс частинки перевищує її ньютонівський імпульс в n = 3 рази.
188. Визначити кінетичну енергію протона, який рухається із швидкістю V= 0,75 С.
189. Визначити роботу, яку необхідно виконати, щоб збільшити швидкість частинки з масою спокою mо від 0.5 С до 0,7 С.
190. Електрон рухається із швидкістю, рівною 0,8 швидкості світла С. Знайти кінетичну енергію електрона:
1) за класичною формулою; 2) за релятивістською. Порівняти результати.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.