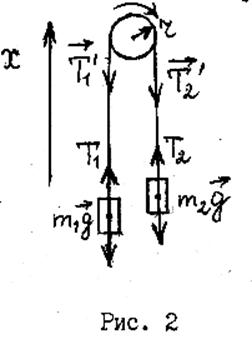
Розв’язання.
Розглянемо сили, що діють на кожний тягарець та на блок окремо.На кожний
тягарець діють дві сили: сила тяжіння та сила пружності ( сила натягу нитки).
Направимо вісь Х вертикально вгору та запишемо для кожного тягарця рівняння руху (П закон Ньютона) в проекціях на вісь Х.
m1а= T1 - mg , (1)
для другого
m2а = m2 g - T2 (2)
Прискорення, з яким рухаються тягарці m1 і m2 однакові, тому що тягарці зв’язані ниткою і складають одну систему. На блок діють Т1 і Т2. Вони приводять до обертання блоку під дією моментів цих сил. Запишемо рівняння обертального руху
(T12 - T11 )r = I e (3)
де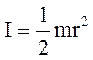 
-
момент інерції блоку, a e =
- кутове прискорення.
Згідно третьому закону Ньютона Т1 = Т11, а Т2 = Т12.
Комбінуючи рівняння (1), (2) і (3), знаходимо
{(m2g - m2а) -
(m1g + m1а)} r = 
mr2 
(4)
звідки
a =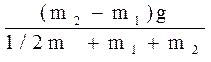
(5)
Після обчислень одержимо а = 2,88 м/с2
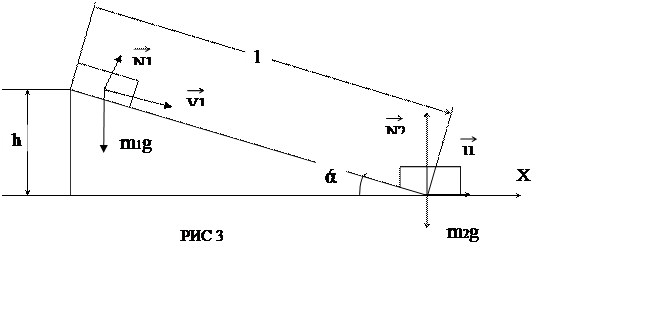
Приклад 4. Вантаж масою m1 = 200 кг ковзає по ідеально гладкій похилій площині довжиною l = 2 м на нерухомий візок з піском і застряє в ньому. Візок з піском масою m2 = 80 кг може вільно (без тертя) рухатись по рейках в горизонтальному напрямку. Визначити швидкість U візка з вантажем. Кут, який утворює похила площина з рейками, дорівнює a = 30о.
Розв'язання. При розв'язанні цієї задачі використовується два закони збереження - закон збереження імпульсу та закон збереження енергії.
Візок та вантаж розглянемо як систему двох непружно взаємодіючих тіл. Ця система не є замкненою, бо на неї діють зовнішні сили: сили тяжіння m1g та m2g та сила реакції N2 (див.рис.3), тому закон збереження імпульсу для системи вантаж - візок застосовувати не можливо. Але ж проекції названих сил на напрямок осі х, яка співпадає з напрямком рейок, дорівнюють нулю, то проекцію імпульсу системи можно вважати постійною
Р1х+Р2х = Р11х +Р12х,
де
Р1х та Р2х - проекції імпульсу вантажу та візка з піском в момент падіння вантажу на візок;
Р11х, Р12хї - ті ж величини після падіння вантажу.
Тіла системи будемо вважати матеріальними точками і запишемо імпульси через їх маси та швидкості, маючи на увазі,
що імпульс візка до взаємодії з вантажем дорівнював нулю (візок покоївся)
Р2х = 0,
крім того після взаємодії обидва тіла системи рухались з однаковою швидкістю U:
m1V1x = (m1+m2) U, (2)
або
m1V1cosa=(m1 +m2) U , (3)
де V1 - модуль швидкості вантажу перед падінням на візок;
V1x = V1 cosa - проекція цієї швидкості на вісь х.
Розв'яжемо останнє рівняння відносно U.
U = m1V1cosa / (m1 +m2) (4)
Модуль швидкості V1 визначимо із закону збереження енергії
m1gh = m1V21,
(5)
де h = lsina, звідки
V1 = 
(6)
Підставимо вираз (6) в рівняння (4) тоді
U =
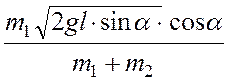
Після розрахунків знайдемо
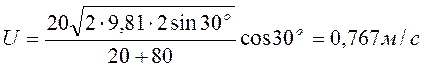
Приклад 5. Маховик у вигляді суцільного диску радіусом R = 0,2 м та масою m = 50 кг обертається з частотою n1 = 480 хв.-1. Під дією сили тертя маховик зупинився через t = 50 с. Визначити момент сили тертя.
Розв'язання. Для розв'язування цієї задачі будемо використовувати основний закон динаміки обертального руху у вигляді
Mz = Iz . 
,
де Mz - момент зовнішніх сил ( в данному випадку момент сили тертя);
Iz - момент інерції маховика (суцільного диску), його визначимо за формулою
Iz = 1/2 mR2,
Dw - змінення кутової швидкості, Dw =w2 - w1. Відомо, що w =2 p n, тоді
Dw = w 2 - w 1 = 2p n2 - 2pn1
Запишемо основний закон, підставивши вирази для I та Dw:
Mz = pmR2(n2 - n1)/Dt
Перевіримо, чи дає отримана формула одиницю моменту сили.
= 
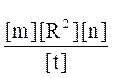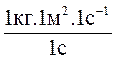= 1кг.м.с-2
. 1 м. = 1 Н.м
Знайдемо числове значення
Mz =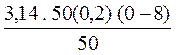
= -1Н.м.
Знак мінус вказує, що момент сил тертя гальмує рух маховика.
Приклад 6. Платформа уявляє собою диск радіусом R = 1,5 м і масою m1 = 180 кг. Вона обертається навколо вертикальної осі з частотою n = 10 хв.-1. В центрі платформи стоїть людина масою m2= 60 кг. Яку лінійну швидкість V відносно підлоги приміщення буде мати людина, якщо вона перейде на край платформи?
Розв'язання. До системи людина - платформа можно застосувати закон збереження моменту імпульсу, тобто
Iz . w = const, (1)
де Iz - момент інерції платформи з людиною відносно осі Z. Момент інерції системи дорівнює сумі моментів інерції тіл, які входять до складу системи, тому в початковому стані
Iz =m1 . R2,
момент інерції людини дорівнює нулю.
В кінцевому стані Iz1 = 1/2 m1R2 + m2R2
Перепишемо рівняння (1)
Iz . w = Iz1 . w1 (2)
Запишемо ще раз закон збереження моменту імпульсу, враховуючи вирази для моментів інерції, а також маючи на увазі, що
w = 2pn, а w1 = V/R (де V - швидкість людини відносно підлоги),
1/2 m1 . R2 . 2pn = ( 1/2 m1R2 + m2R2) . V/R.
З цього рівняння визначимо V .
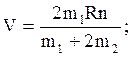
Після розрахунку одержимо V= 0,3 м/с.
Контрольна робота № 1
101. Рівняння прямолінійного руху має вигляд
x = At + Bt2 ,
де А = 3 м/с; В = -0,25 м/с2. Накреслити графіки залежності координати і швидкості від часу.
102. Рух матеріальної точки задано рівнянням
х = Аt + Bt2,
де А = 4 м/с; В = -0,5 м/c2.
В який момент часу швидкість точки V дорівнює нулю? Знайти координату і прискорення в цей момент.
103. Автомобіль проїхав першу половину відстані з швидкістю 40 км/год, другу - з швидкістю 60 км/год. Знайти середню швидкість на всій відстані.
104. Камінь падає з висоти h =1200 м. Який шлях S пройде камінь за останню секунду свого падіння?
105. Діти перекидаються м'ячем. На яку максимальну висоту він піднімається , якщо час польоту від хлопчика до хлопчика дорівнює 2 с?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.