Кінетична енергія фотоелектрона може бути знайдена за класичною формулою (3), тому що енергія фотона e1 (8 еВ ) значно менша, ніж енергія спокою електрона Ео = 0,51 МеВ.
Знайдемо Vmax =
(5)
Обчислення дають
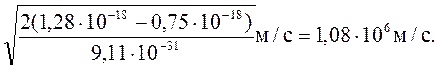
2. Обчислення енергії g - фотона дає значення
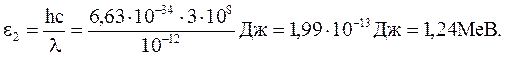
Робота виходу електрона з поверхні срібла (А = 4,7 еВ = 0,75 . 10-18 Дж) значно меньша в порівнянні з енергією g - фотона Е2 , тому можна прийняти, що максимальна кінетична енергія електрона дорівнює енергії фотона Тmax = e2 = 1,24 МеВ. В даному разі для обчислення Vmax треба брати релятивістську формулу (4).
.
Врахувавши, що Т =Тmax = e2, знайдемо
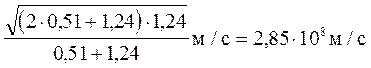
Приклад 8. У результаті ефекту Комптона фотон при зіткненні з e=0,4 електроном був розсіяний на кут J = 90о. Енергія розсіяного фотона e2 = 0,4 МеВ. Знайти енергію фотона до розсіювання.
Для визначення енергії первинного фотона скористаємось формулою Комптона
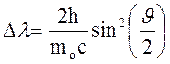(1)
- зміна довжини хвилі фотона в
результаті розсіювання на вільному електроні; mо - маса спокою електрона ; с - швидкість
світла у вакуумі; J- кут розсіювання
фотона.
Використавши формулу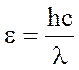 
, запишемо довжини
хвиль l1 і l2 через енергії фотонів, а домноживши чисельник та знаменник правої
частини формули (1) на с, отримаємо
.
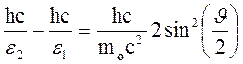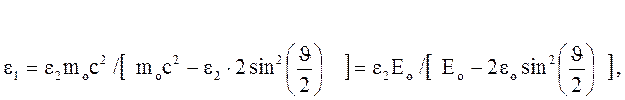
де Ео = moc2 =0,511 МеВ - енергія спокою електрона.
Енергію Е1 обчислимо у мегаелектронвольтах
e1
=
Приклад 9. Пучок монохроматичного світла з довжиною хвилі l = 663 нм падає нормально на дзеркальну плоску поверхню. Потік енергії в одиницю часу Фе = 0,6 Вт. Знайти : 1) силу тиску F на поверхню; 2) число фотонів, що падають на поверхню кожну секунду.
Розв’язання
Сила світлового тиску на поверхню дорівнює
F = P . S, (1)
де Р – тиск; S – площа поверхні.
Світловий тиск можна знайти за формулою
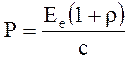, (2)
де Ео - енергетична освітленість; c - швидкість світла у вакуумі; r- коефіцієнт відбивання.
Після підстановки формули (2) у формулу (1) отримаємо
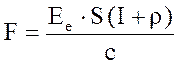(3)
Сила тиску також дорівнює
(4)
тому що Ее . S = Фе.
Для дзеркальної поверхні r = 1, після підстановки отримаємо
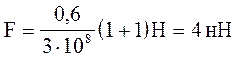
2. Добуток енергії e одного фотона на число фотонів n, що падають на поверхню кожну секунду, дорівнює потужності
випромінювання, тобто потоку випромінювання Фе = en.
Використаємо зв’язок між довжиною хвилі та енергією фотона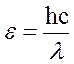 
і після підстановки отримаємо
Фе= hcn/l.
З цієї
формули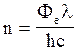 
Після
обчислення маємо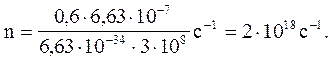 
501. У досліді Юнга відстань між щілинами d =1 мм, а відстань від щілин до екрану рівна 3 м. Визначити: 1) розташування першої світлої смуги; 2) розташування третьої темної смуги, якщо щілини освітлювати монохроматичним світлом з довжиною хвилі l = 0,5 мкм.
502. На скляний клин вертикально падає монохроматичне світло довжиною хвилі 0,6 мкм. Число інтерференційних смуг, які приходяться на l = 1 см, рівне 10. Визначити заломлюючий кут клину.
503. Пучок монохроматичних ( l = 0,6 мкм) світлових хвиль падає під кутом і = 30о на мильну плівку, яка знаходиться в повітрі. При якій найменшій товщині d плівки відбиті світлові пучки будуть максимально ослаблені інтерференцією? Максимально підсилені?
504. В інтерферометрі Жамена дві однакові трубки довжиною l = 15 см були заповнені повітрям з показником заломлення 1,000292. Коли в одній з трубок повітря замінили ацетиленом, то інтерференційна картина змістилась на 80 смуг. Визначити показник заломлення n2 ацетилену, якщо в інтерферометрі використовувалось джерело монохроматичного світла з довжиною хвилі l = 0,590 мкм.
505. Визначити радіуси трьох перших світлих кілець Ньютона, отриманих у відбитому світлі, при освітленні системи жовтим полум’ям натрію (l = 0,589 мкм), яке падає на лінзу нормально. Радіус кривизни лінзи 3,6 м. Прошарок між лінзою і пластиною заповнено водою.
506. Для зменшення коефіцієнту відбиття світла від оптичних стекол їх покривають тонкою плівкою речовини з показником заломлення n = 1,22 , меншим ніж у скла. При якій товщині плівки відбиття світла буде рівне нулю? Довжина хвилі світла 0,500 мкм, кут падіння променів 70о.
507. Визначити товщину повітряного прошарку між плоско-опуклою лінзою і плоскою скляною пластиною в тому місці, де знаходиться п’яте світле кільце, якщо спостереження ведеться: 1) у відбитому світлі l= 0,6 мкм, 2) у світлі, яке проходить.
508. На екрані спостерігається інтерференційна картина в результаті накладання променів від двох когерентних джерел ( l =500 нм). На шляху одного з променів перпендикулярно йому помістили скляну пластину (n = 1.6) товщиною d = 5 мкм. Визначити, на скільки смуг зміститься при цьому інтерференційна картина.
509. Визначити довжину l1 відрізка, на якому укладається стільки ж довжин хвиль у вакуумі, скільки їх укладається на відрізку l2 = 3 мм у воді. Скільки довжин хвиль монохроматичного світла з частотою коливань n = 5 . 1014 Гц укладається на відрізку l1 у вакуумі?
510. Відстань d між когерентними джерелами світла рівна 0,5 мм.
Відстань від джерел до екрану рівна 5 м. У жовтому світлі ширина інтерференційних смуг дорівнює 6 мм. Знайти довжину хвилі жовтого світла.
511. На діафрагму з круглим отвором радіусом r = 1,5 мм падає нормально монохроматична хвиля (l = 0,5 мкм). На екрані, віддаленому від діафрагми на 1,5 м, спостерігається дифракційна картина. Темна чи світла пляма буде спостерігатися в центрі дифракційної картини? Визначити радіус другої зони Френеля.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.