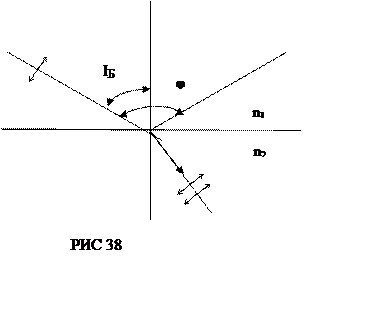
Приклад 3. Пучок природного світла падає на поліровану поверхню скляної пластини, зануреної в рідину. Відбитий від пластини пучок світла утворює кут j = 97о з падаючим пучком. Знайти показник заломлення n1 рідини, якщо відбитий пучок максимально поляризований (рис. 38)
 Розв’язання
Розв’язання
![]()
![]() По закону Брюстера пучок світла, відбитий
від діелектрика, максимально поляризований у тому випадку, коли тангенс кута
падіння дорівнює відносному показнику заломлення другого середовища (скла)
відносно першого (рідини)
По закону Брюстера пучок світла, відбитий
від діелектрика, максимально поляризований у тому випадку, коли тангенс кута
падіння дорівнює відносному показнику заломлення другого середовища (скла)
відносно першого (рідини)
![]() tqiБ = n21 = n2/n1.
tqiБ = n21 = n2/n1.
іБ = j/2, тому що кут падіння дорівнює куту відбивання. Таким чином, n1 = n2/tq (j/2)
Обчислення дають
n1 =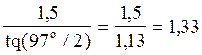
|
|
|
|
|
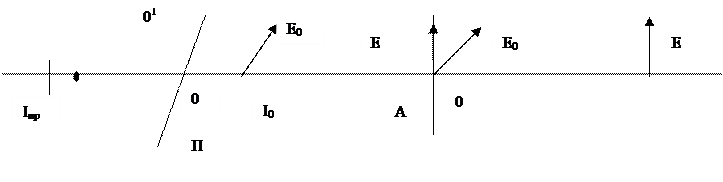 |
РИС 39
1. Природне світло у поляроїді розбивається
на два поляризованих пучки: звичайний та незвичайний. Звичайний пучок у
поляроїді поглинається, тому з поляроїду виходить незвичайний пучок з
інтенсивністю Іо = Іпр/2. Напрямок коливань вектора ![]() незвичайного пучка паралельний
оптичній осі 00¢ поляроїду (рис.39).
незвичайного пучка паралельний
оптичній осі 00¢ поляроїду (рис.39).
Крім того, завдяки поглинанню світла, з коефіцієнтом поглинання k, інтенсивність незвичайного пучка в поляроїді ще зменшується, тобто стає меншою, ніж 1/2 І пр.
Таким чином, інтенсивність світла, що вийшло із першого поляроїду (поляризатора П), дорівнює
Io 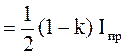 (1)
(1)
Щоб отримати відповідь, необхідно інтенсивність природнього світла Іпр поділити на інтенсивність Іо світла, що вийшло з поляроїда (1).
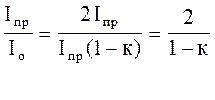 (2)
(2)
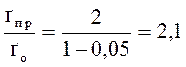
2. Плоскополяризований пучок світла інтенсивності Іо падає на другий поляроїд, розділяється на два пучки, один з яких - звичайний - в поляроїді поглинається. Інтенсивність незвичайного пучка зменшується за законом Малюса та внаслідок поглинання у рідині має вигляд:
І = Іо(1 - k) cos2a,
де І - інтенсивність світла, що вийшло з другого поляроїду ( аналізатора А ).
Поділивши Іпр на І, враховуючи (1), отримаємо відповідь на друге питання задачі
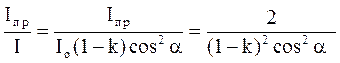
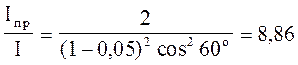 .
.
Приклад 5. Плоскополяризований монохроматичний пучок світла падає на поляроїд і повністю ним гаситься. Коли на шляху пучка розташували кварцеву пластинку, інтенсивність І пучка світла після поляроїду стала дорівнювати половині інтенсивності пучка, що падає на поляроїд. Знайти товщину цієї кварцевої пластини. Сталу обертання a кварцу прийняти рівною 48,9 град/мм.
Розв’язання
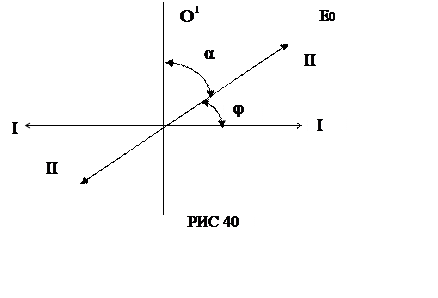 Повне гасіння світла поляроїдом означає, що оптична вісь
поляроїду (лінія 00¢ на рис.40)
перпендикулярна напрямку коливань І-І вектора
Повне гасіння світла поляроїдом означає, що оптична вісь
поляроїду (лінія 00¢ на рис.40)
перпендикулярна напрямку коливань І-І вектора ![]() плоскополяризованого
світла, падаючого на нього. Кварцева пластина повертає площину коливань світла
на кут j
плоскополяризованого
світла, падаючого на нього. Кварцева пластина повертає площину коливань світла
на кут j
j = a . d (1)
|
де d - товщина пластини.
|
Використаємо
залежність 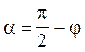 (див. рис.40) і отримаємо
(див. рис.40) і отримаємо
І = Іоcos2 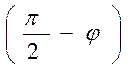 або І = Іоsin2φ (2)
або І = Іоsin2φ (2)
Після підстановки (1) у (2) із рівняння (2) знайдемо
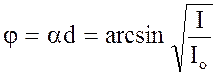 ;
;
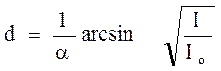 .
.
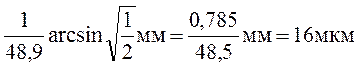 .
.Приклад 6. Довжина хвилі, на яку припадає максимум спектральної світності у спектрі випромінювання чорного тіла, lmax = 0,58 мкм. Знайти інтегральну енергетичну світність R чорного тіла
Енергетична світність R абсолютно чорного тіла відповідно закону Стефана-Больцмана пропорційна четвертій степіні термодинамічної температури
R = sT4, (1)
де s - стала Стефана - Больцмана.
Температуру Т можна обчислити за законом зміщення Віна
lm = b/Т, (2)
де b – стала Віна.
Використавши (1) і (2), знайдемо
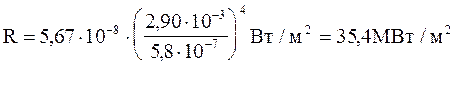
Приклад 7. Знайти максимальну швидкість Vmax фотоелектронів, які вириваються з поверхні срібла: 1) ультрафіолетовим випромінюванням з довжиною хвилі l1 = 0,155 мкм; 2) g - випромінюванням з довжиною хвилі l2 = 1 пм.
Максимальну швидкість фотоелектронів можна знайти з рівняння Ейнштейна для фотоефекту
e = hn = А + Т, (1)
де e - енергія падаючого фотона ; А - робота виходу фотоелектрона з металу (див.табл); Т - його кінетична енергія .
Енергію фотона можна також обчислити по формулі
e = hс/l, (2)
де h - стала Планка; с - швидкість світла у вакуумі; l - довжина хвилі випромінювання.
Кінетична енергія електрона визначається класичною формулою
T = mo V2max/2 , (3)
де mo – маса спокою електрона
або релятивістською формулою
Т = 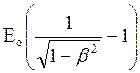 , (4)
, (4)
де Ео = moc2 - енергія спокою електрона ; b = Vmax/c,
в залежності від швидкості фотоелектрону. Якщо енергія фотона є того ж порядку, як енергія спокою Ео електрона, то треба використовувати формулу (4).
1. Обчислення енергії ультрафіолетового фотона за формулою (2) дає значення
e1 =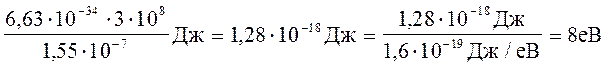
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.