4 ЕЛЕКТРОМАГНЕТИЗМ. КОЛИВАННЯ І ХВИЛІ
Основні формули
Закон Біо-Савара -Лапласа
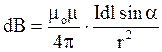 ,
,
де dB - магнітна індукція поля, утвореного елементом провідника d![]() з струмом I; r - радіус -вектор точки, в якій визначається магнітна індукція; a - кут між елементом струму і радіус-вектором; mо
- магнітна стала; m - магнітна проникність.
з струмом I; r - радіус -вектор точки, в якій визначається магнітна індукція; a - кут між елементом струму і радіус-вектором; mо
- магнітна стала; m - магнітна проникність.
Зв’язок магнітної індукції В з напруженістю Н магнітного поля
В =![]() .
.
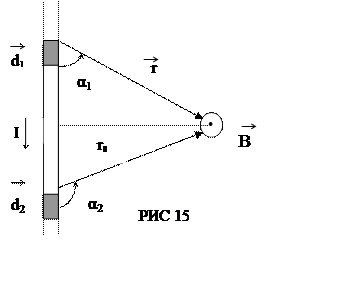 Магнітна індукція
поля, утвореного відрізком провідника із струмом (рис. 15)
Магнітна індукція
поля, утвореного відрізком провідника із струмом (рис. 15)
![]()
 .
.
Магнітна індукція поля прямого нескінченно довгого провідника із струмом
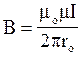 .
.
Магнітна індукція в центрі кругового струму
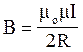 .
.
Магнітна індукція на осі кругового струму
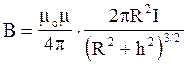 ,
,
де h - віддаль від центра витка до точки, в якій визначається магнітна індукція.
Магнітна індукція нескінченно довгого соленоїду
![]() ,
,
де n - число витків на одиницю довжини.
Магнітний момент контура із струмом
Pm = I . S
Механічний (обертаючий) момент, який діє на контур із струмом, розміщений в однорідному магнітному полі,
M = PmBsina,
де a - кут між Рm і В.
Потенціальна енергія (механічна) контура із струмом в магнітному полі
Еn = - Рm Bcosa.
Відношення магнітного моменту Рm до моменту імпульсу L зарядженої частинки, що рухається в магнітному полі по круговій орбіті,
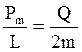 ,
,
де Q – заряд; m - маса частинки.
Закон Ампера для однорідного магнітного поля
F = IBlsina,
де ![]() - довжина провідника; a - кут між напрямом струму і вектором магнітної
індукції В.
- довжина провідника; a - кут між напрямом струму і вектором магнітної
індукції В.
Сила взаємодії двох нескінченно довгих паралельних провідників із струмом
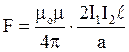 .
.
Сила Лоренца F = QVBsina,
де V - швидкість зарядженої частинки; a - кут між ![]()
Магнітний потік
а) для однорідного магнітного поля і плоскої поверхні
Ф = В . S cosa
б) для неоднорідного поля і любої поверхні
Ф =![]() ,
,
Потокозчеплення (повний потік)
Y = N . Ф
Робота при переміщенні замкнутого контура із струмом в магнітному полі
А =ІDФ.
Основний закон електромагнітної індукції (закон Фарадея)
eі=
- N 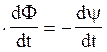 .
.
Е.Р.С. самоіндукції
esi = - L![]() .
.
Різниця потенціалів на кінцях провідника, що рухається в магнітному полі з швидкістю V,
U = BlVsina.
Заряд, який проходить по замкнутому контуру при зміні магнітного потоку через цей контур,
Q =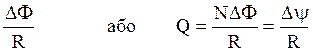
Індуктивність соленоїда
L =momn2V,
де n - число витків на одиницю довжини; V - об’єм соленоїда.
Миттєве значення сили струму кола, яке має опір R і індуктивність L
а) при замиканні кола
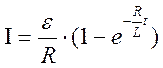
б) при розмиканні кола
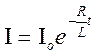
Енергія магнітного поля
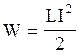
Об’ємна густина енергії магнітного поля
![]()
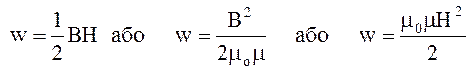 .
.
Кінетичне рівняння гармонійних коливань матеріальної точки
x = A сos(wt +j),
де А – амплітуда; w - циклічна частота; j - початкова фаза коливань; х - зміщення.
Швидкість при гармонійних коливаннях дорівнює
![]() V = -
Awsin(wt + j),
V = -
Awsin(wt + j),
прискорення
![]() = а = - Аw2cos(wt +j).
= а = - Аw2cos(wt +j).
Період коливання:
а) фізичного маятника
Т = 2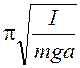 ,
,
б) пружинного маятника
Т = 2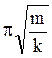 ,
,
в) математичного маятника
Т = 2![]() .
.
Енергія гармонійних коливань
Е 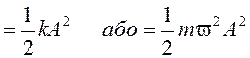 .
.
Період електромагнітних коливань в контурі Томсона
![]() .
.
Кінетичне рівняння згасаючих електромагнітних коливань
Q = Aoe-btcos(wt +j),
де b =![]() - коефіцієнт
згасання.
- коефіцієнт
згасання.
Логарифмічний декремент згасання
l=bТ
Швидкість електромагнітних хвиль в середовищі
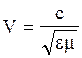 ,
,
де ![]() e - діелектрична проникність, m - магнітна проникність середовища.
e - діелектрична проникність, m - магнітна проникність середовища.
Приклади розв'язування задач
Приклад 1.
По відрізку прямого провідника, довжина якого ![]() = 80 см, тече струм І = 50 А. Визначити
магнітну індукцію В поля, утвореного цим струмом в точці А, рівновіддаленій
від кінців відрізка провода, яка знаходиться на відстані rо = 30 см від його середини.
= 80 см, тече струм І = 50 А. Визначити
магнітну індукцію В поля, утвореного цим струмом в точці А, рівновіддаленій
від кінців відрізка провода, яка знаходиться на відстані rо = 30 см від його середини.
Розв’язання
Для розв’язування задачі скористуємось законом
Біо-Савара-Лапласа і принципом суперпозиції магнітних полів. Закон
Біо-Савара-Лапласа дозволяє визначити магнітну індукцію dB, створювану елементом струму Idl. Помітимо, що вектор
![]() в точці А спрямований за площину
рисунка. Принцип суперпозиції дозволяє для визначення
в точці А спрямований за площину
рисунка. Принцип суперпозиції дозволяє для визначення ![]() скористуватися
інтегруванням
скористуватися
інтегруванням
![]()
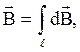 (1)
(1)
|
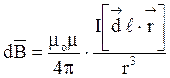 ,
,
де d![]() - магнітна
індукція, утворена елементом провідника, довжина якого dl із струмом I в точці,
визначеній радіусом-вектором
- магнітна
індукція, утворена елементом провідника, довжина якого dl із струмом I в точці,
визначеній радіусом-вектором ![]() ;
;
mо - магнітна стала
m
- магнітна проникність
середовища, в якому знаходиться провід ( в нашому випадку m = 1). Помітимо, що вектори d![]() від різних елементів струму співнаправлені (рис. 16), тому вираз (1)
можна переписати в скалярній формі
від різних елементів струму співнаправлені (рис. 16), тому вираз (1)
можна переписати в скалярній формі
![]() ,
,
де
dB =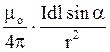
В скалярному виразі закону Біо-Савара-Лапласа кут a є кут між елементом струму Id![]() і радіусом-вектором
і радіусом-вектором ![]() . Таким чином,
. Таким чином,
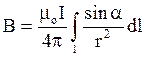 (2)
(2)
Перетворимо підінтегральний вираз так, щоб була одна перемінна - кут a. Для цього виразимо довжину елемента провода dl через кут da (рис.16)
dl =![]()
Тоді підінтегральний вираз![]() запишемо в
вигляді
запишемо в
вигляді
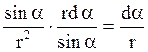
Помітимо, що перемінна r також залежить від a (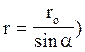 ,
,
отже 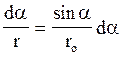
Таким чином, вираз (2) можна переписати у вигляді
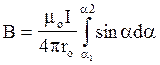 ,
,
де a1 і a2 границі інтегрування.
Виконаємо інтегрування 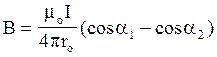 (3)
(3)
Помітимо, що при симетричному розташуванні точки А відносно відрізка провода, cosa2 = -cos a1. З урахуванням цього формула (3) приймає вигляд
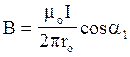 (4)
(4)
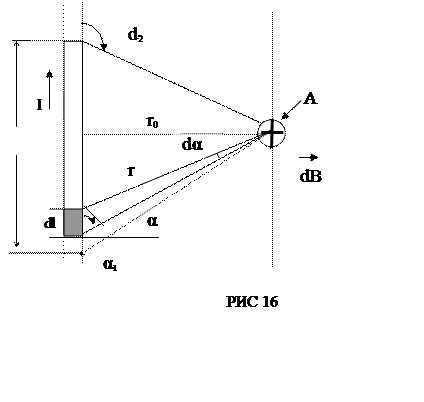
З рис. 16 виходить
сosa1 = 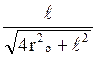
Підставивши вираз cosa1 в формулу (4), одержимо
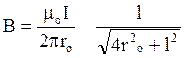 (5)
(5)
Виконавши обчислення по формулі (5), знайдемо В = 26,7 мкТл. Напрям вектора магнітної індукції В поля, утворюваного прямим струмом, можна визначити по правилу буравчика ( правилу правого гвинта). Вектор магнітної індукції В в точці А (рис. 16) направлений перпендикулярно площині рисунка від нас.
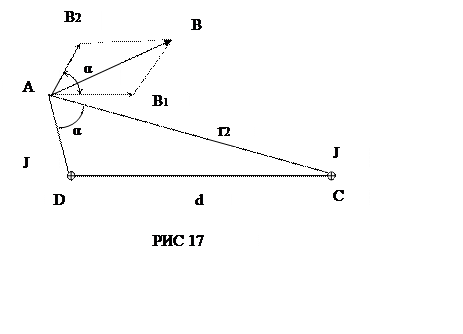
Приклад 2. Два паралельних нескінченно довгих провода D і С, по яких течуть в одному напрямку електричні струми, сила яких І = 60 А, розташовані на відстані d = 10 см один від одного. Визначити магнітну індукцію В поля, утворюваного провідниками із струмом в точці А (рис. 17), яка знаходиться від осі одного провідника на відстані r1 = 5 cм, від другого -r2 = 12 cм.
![]()
![]()
![]()
 Розв’язання
Розв’язання
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.