Розв’язання
При виключенні магнітного поля трапиться зміна магнітного потоку. Внаслідок цього в рамці виникне Е.Р.С. індукції , обумовлена основним законом електромагнітної індукції
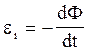
Виникаюча Е.Р.С. індукції викличе в рамці індукційний струм, миттєве значення якого можна визначити, скориставшись законом Ома
Іі 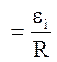 ,
,
де R - опір рамки. Тоді
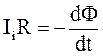
Миттєве значення сили
індуктивного струму 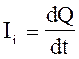 , цей вираз можна
переписати у вигляді
, цей вираз можна
переписати у вигляді 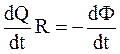 ,
,
звідки dQ =
-![]() (1)
(1)
Проінтегрувавши вираз (1), знайдемо
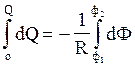 або
або 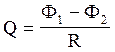
При виключеному полі
(кінцевий стан) Ф2 = 0, остання рівність перепишеться в
вигляді 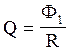 (2)
(2)
Знайдемо магнітний потік Ф1. За визначенням магнітного потоку маємо
Ф1 = В . S . сos a,
де S - площа рамки.
В нашому випадку (рамка квадратна)
S = а2 . Тоді Ф1 = Ва2cosa. (3)
Підставивши (3) в
(2), одержимо 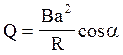
Переконаємось в тому, що права частина цієї рівності дає одиницю заряду (Кл):
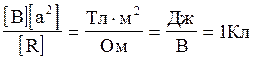
Виконаємо обчислення:
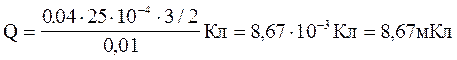
Приклад 11. Соленоїд з сердечником з немагнітного матеріалу вміщує N = 1200 витків проводу, щільно прилеглих один до одного. При силі струму І = 4 А магнітний потік Ф = 6 мкВб.
Визначити індуктивність L соленоїду і енергію W магнітного поля соленоїду.
Розв’язання
Індуктивність L зв’язана з потокозчепленням y і силою струму І співвідношенням
y = LI (1)
Потокозчеплення, в свою чергу, може бути визначене через потік Ф і кількість витків N (при умові, що витки щільно прилягають один до одного )
Y = NФ (2)
З формул (1) і (2) знаходимо індуктивність соленоїду
L =![]() (3)
(3)
Енергія магнітного поля соленоїду
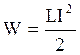
Виразивши L згідно (3), одержимо
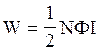 (4)
(4)
Підставимо в формули (3) і (4) значення фізичних величин і виконаємо обчислення
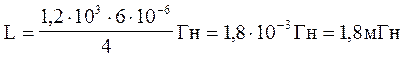
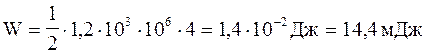
Приклад 12. Точка здійснює гармонійне коливання з частотою n = 10 Гц. В момент, прийнятий за початок, точка мала максимальне зміщення:
Xmax =1 мм
Написати рівняння коливань точки і накреслити їх графік
Розв’язання
Рівняння коливань можна записати в вигляді
х = Аsin(wt +j), (1)
де А - амплітуда коливань; w - циклічна частота; t - час; j - початкова фаза.
По визначенню, амплітуда коливань
А = Хmax (2)
Циклічна частота w зв’язана з частотою n співвідношенням
w = 2pn (3)
Для моменту часу t = 0 формула (1) приймає вигляд
Xmax = Asinj
звідки початкова фаза
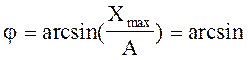 (1)
(1)
або j = (2к + 1) p/2 (К = 0, 1, 2,...)
Зміна фази на 2p не змінює становища коливальної точки, а тому можна
прийняти j =![]() (4)
(4)
З врахуванням рівнянь (2) - (4) рівняння коливань матиме вигляд
x = Asin(2pnt + ![]() або x = Acos2pnt,
або x = Acos2pnt,
де А = 1 мм = 10-3 м; n = 10 Гц; 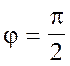
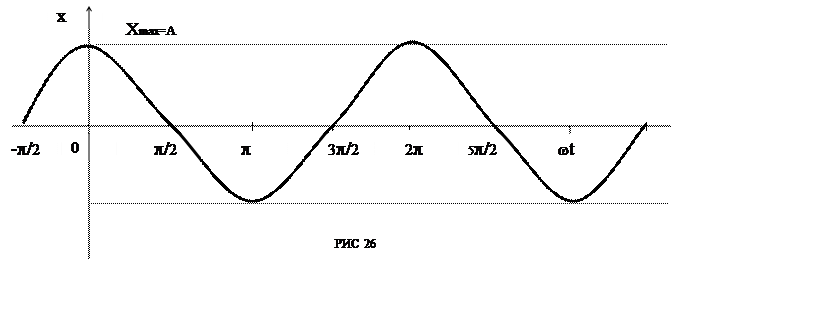
Графік відповідного гармонійного коливання приведений на рис. 26.
Приклад 13. Частинка, маса якої m = 0,1 кг, здійснює гармонійне коливання з періодом Т = 2 с. Повна енергія коливальної частинки Е = 0.1 мДж. Визначити амплітуду А коливань і найбільше значення сили Fmax, діючої на частинку.
Розв’язання
Для визначення амплітуди коливань скористаємось виразом повної енергії
частинки 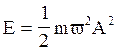 ,
,
де 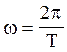 . Звідси амплітуда
. Звідси амплітуда
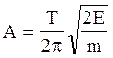 (1)
(1)
Якщо частинка здійснює гармонійне коливання, то сила, яка діє на неї, являється квазіпружною і, отже, може бути виражена співвідношенням F = -kx, де k - коефіцієнт квазіпружної сили;
х - зміщення коливальної точки. Максимальною сила буде при максимальному зміщенні x max, рівному амплітуді:
Fmax = kA (2)
Коефіцієнт k виразимо через період коливань:
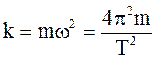 (3)
(3)
Підставивши вираз (1) і (3) в (2) і виконавши спрощення, одержимо
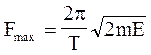
Виконаємо обчислення:
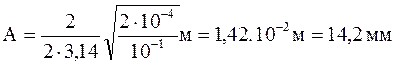
Fmax =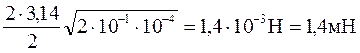
Приклад 14. Плоска хвиля поширюється вздовж прямої із швидкістю V = 20 м/с. Дві точки, які знаходяться на цій прямій на відстанях х1 = 12 м і х2 = 15 м від джерела хвиль, коливаються з різницею фаз Dj = 0,75 p. Знайти довжину хвилі l, написати рівняння хвилі і знайти зміщення указаних точок в момент t = 1,2 с; якщо амплітуда коливань А = 0,1 м.
Розв’язання
Точки, які знаходяться одна від другої на відстані, яка дорівнює довжині хвилі l, коливаються з різницею фаз, рівною 2p; точки, які знаходяться одна від одної на любій відстані Dх, коливаються з різницею фаз, рівною
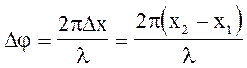 (1)
(1)
Розв’язуючи це рівняння відносно l, одержимо
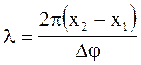 (2)
(2)
Підставивши числові
значення величин, які входять в вираз (2) і виконавши арифметичні дії,
одержимо: 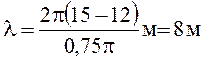
Для того, щоб написати рівняння плоскої хвилі, потрібно ще знайти
частоту w: 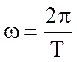 ,
,
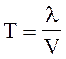 ,
,
тоді
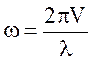
Виконаємо обчислення:
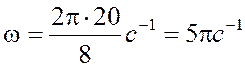
Знаючи амплітуду А коливань, циклічну частоту w і швидкість V розповсюдження хвилі, можна написати рівняння плоскої хвилі для даного випадку;
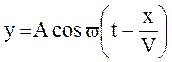 ,
(3)
,
(3)
де А = 0,1 м; w = 5 pс-14; V = 20 м/с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.