![]() , (1)
, (1)
де a - кут між векторами ![]() 1
і
1
і ![]() 2.
2.
Магнітні індукції В1 і В2 виражаються відповідно через силу струму І і відстані r1 i r2 від проводів до точки А
В1 =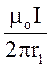 ,
,
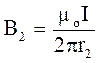
Підставляючи вирази В1
і В2 в формулу (1) і виносячи ![]() за
знак кореня, одержуємо
за
знак кореня, одержуємо 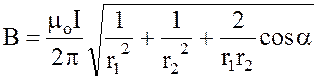 (2)
Обчислимо cosa.
Помітивши, що a =<DАС ( як кути з відповідно перпендикулярними
сторонами), за теоремою косинусів запишемо
(2)
Обчислимо cosa.
Помітивши, що a =<DАС ( як кути з відповідно перпендикулярними
сторонами), за теоремою косинусів запишемо
d2 = r12 +r22 – 2 r1r2 cosa,
де d - відстань між провідниками.
сos a =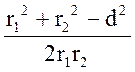
cos a =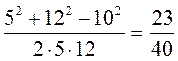
Підставимо в формулу (2) числові значення фізичних величин і виконаємо обчислення
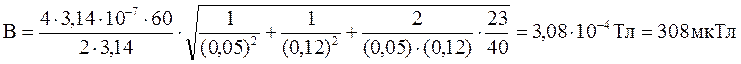
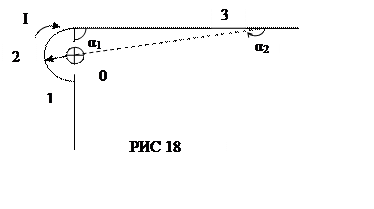
Приклад 3. Нескінченно довгий провідник зігнутий так, як це зображено на рис.18. Радіус R дуги дорівнює 10 см. Визначити магнітну індукцію В поля, яке утворене в точці 0 струмом І = 80 А, що протікає по цьому провіднику.
Розв’язання
|
|
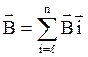 .
.
В нашому випадку провід можно розділити на три частини (1, 2, 3):
два прямолінийних
провода (1 і 3), які одним кінцем переходять в нескінченність, і дугу півкола
(2) радіусом R. Тоді ![]() ,
,
де В1, В2,
В3 - магнітні індукції в точці 0 , утворювані струмом ,який тече
відповідно на першій, другій і третій ділянках провода. Точка 0 лежить на осі
провода 1, то В1 = 0 і тоді ![]() +
+![]()
Враховуючи, що
вектори ![]() і
і ![]() направлені
відповідно правилу буравчика перпендикулярно площині рисунка від нас, то
геометричне інтегрування можна замінити алгебраїчним
направлені
відповідно правилу буравчика перпендикулярно площині рисунка від нас, то
геометричне інтегрування можна замінити алгебраїчним
В = В2 + В3
Магнітну індукцію В2 знайдемо, скористувавшись виразом для магнітної індукції в центрі кругового струму
В2 =![]()
В нашому випадку магнітне поле в точці 0 утворюється лише половиною такого кругового струму, тому
В2 =![]()
Магнітну індукцію В3 знайдемо, скористувавшись співвідношенням (3), яке виведене в прикладі І:
В = 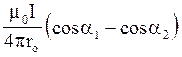
В нашому випадку rо
= R, 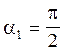 i cosa1 = 0
i cosa1 = 0
a2 = p і cos a2 = -1
Тоді
В3 =![]()
Використавши знайдений вираз для В2 і В3, одержимо
В = 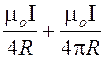 або
В=
або
В=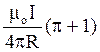
Виконаємо обчислення:
В = 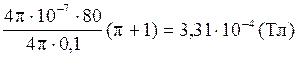
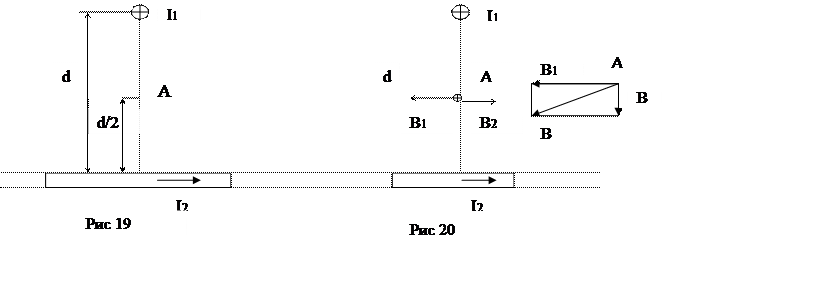 Приклад 4. Два
нескінченно довгих провода схрещені під прямим кутом (рис.19). По проводах
течуть струми І1 = 80 А і І2 = 60 А. Відстань між
проводами дорівнює 10 см. Визначити індукцію
Приклад 4. Два
нескінченно довгих провода схрещені під прямим кутом (рис.19). По проводах
течуть струми І1 = 80 А і І2 = 60 А. Відстань між
проводами дорівнює 10 см. Визначити індукцію ![]() в
точці А, однаково віддаленій від обох проводів.
в
точці А, однаково віддаленій від обох проводів.
Розв’язання
Відповідно
з принципом суперпозиції магнітних полів магнітна індукція ![]() поля, утворюваного струмами І1
і І2, визначається виразом
поля, утворюваного струмами І1
і І2, визначається виразом ![]() ,
де
,
де ![]() - магнітна індукція поля, утвореного
в точці А струмом І1;
- магнітна індукція поля, утвореного
в точці А струмом І1;
![]() - магнітна індукція поля, утвореного
в точці А струмом І2.
- магнітна індукція поля, утвореного
в точці А струмом І2.
Помітимо, що вектори
![]() і
і ![]() взаємно
перпендикулярні (їх напрямки знаходяться за правилом буравчика і зображені в
двох проекціях на рис.20). Тоді модуль вектора можна визначити за теоремою Піфагора
взаємно
перпендикулярні (їх напрямки знаходяться за правилом буравчика і зображені в
двох проекціях на рис.20). Тоді модуль вектора можна визначити за теоремою Піфагора
В = /![]() / =
/ = ![]() ,
,
де В1 і В2 визначаються за формулами розрахунку магнітної індукції для нескінчено довгого прямолінійного провідника із струмом
В1 = 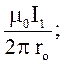 В2
=
В2
=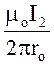
В нашому випадку rо
=![]()
В =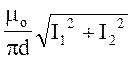
Виконаємо обчислення
В =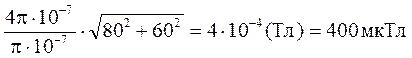
Приклад 5. По двох паралельних прямих провідниках , довжина яки l = 2,5 м кожний, які знаходяться на відстані d = 20 см один від одного, течуть однакові струми І = 1 кА. Визначити силу взаємодії струмів.
Розв’язання Взаємодія двох провідників, по яких течуть струми, здіснюється через
магнітне поле. Кожний струм утворює магнітне поле, яке діє на другий провідник.
Припустимо, що обидва струми (позначимо їх для зручності І1 і І2)
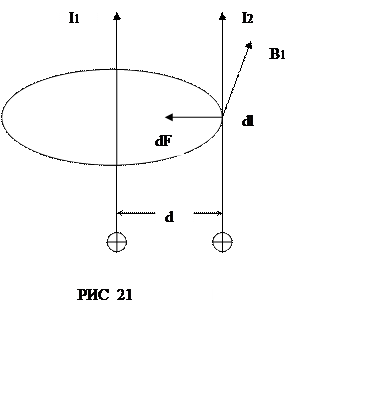 течуть в одному напрямку.
Струм І1 утворює в місці розташування другого провідника (із струмом
І2) магнітне поле. Проведемо лінію магнітної індукції (пунктир на
рис.21) через другий провідник і по дотичній до неї - вектор магнітної індукції
течуть в одному напрямку.
Струм І1 утворює в місці розташування другого провідника (із струмом
І2) магнітне поле. Проведемо лінію магнітної індукції (пунктир на
рис.21) через другий провідник і по дотичній до неї - вектор магнітної індукції
![]() . Модуль магнітної індукції В1
визначається співвідношенням
. Модуль магнітної індукції В1
визначається співвідношенням
В1 =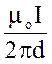 (1)
(1)
Згідно закону Ампера на кожний елемент другого проводу із струмом І2, довжина якого dl, в магнітному полі діє сила
dF = I2B1dl .
sin (![]() 1)
1)
Вектор d![]() перпендикулярний вектору
перпендикулярний вектору ![]() 1 і sin(d
1 і sin(d![]() 1) = 1, тоді
1) = 1, тоді
dF = I2B1dl,
Підставивши в цей вираз В1 згідно (1), одержимо
dF = 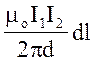
Силу F взаємодії проводів зі струмом знайдемо інтегруванням:
F =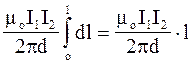
Помітивши, що І1 = І2 =І, одержимо
F =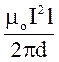
Переконаємось в тому, що права частина цієї рівності дає одиницю сили (Н):
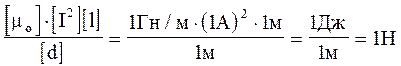
Виконаємо обчислення:
F=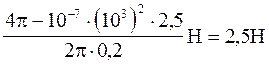
Сила F співнаправлена з силою dF (рис. 21) і визначається в даному випадку простіше правилом лівої руки.
Приклад 6. Протон, який пройшов прискорюючу різницю потенціалів U = 600 В, влетів в однорідне магнітне поле з індукцією В = 0,3 Тл і почав рухатися по колу. Визначити радіус R кола.
Розв’язання
Рух
зарядженої частинки в однорідному магнітному полі буде проходити по колу тільки
в тому випадку, коли частинка влітає в магнітне поле перпендикулярно лініям
магнітної індукції ![]() .
.
Сила Лоренца
перпендикулярна вектору ![]() і надає частинці
(протону) нормальне прискорення аn.
і надає частинці
(протону) нормальне прискорення аn.
Згідно другому закону Ньютона,
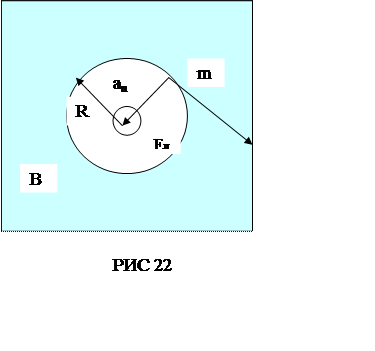
![]() , (1)
, (1)
де m - масса протона.
![]()
![]()
![]()
![]()
|
Перепишемо вираз (1) в скалярній формі (в проекції на радіус)
Fл = man (2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.