Електромагнетизм. Коливання і хвилі, страница 3

В скалярній формі F_л = QVBsina, в нашому випадку   і sin a =1 ¸ тоді         F_л= QVB.

Нормальне прискорення  а_n=, тоді вираз (2) перепишемо таким чином

QVB = .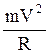

Звідси знаходимо радіус кругової троєкторії

R =.

Помітивши, що  mV є імпульсом протона (Р), цей вираз можна записати в вигляді

R =               (3)

Імпульс протона знайдемо, скориставшись зв’язком між роботою сил електричного поля і зміненням кінетичної енергії протона, тобто

А =D Т    або    Q(j₁ - j₂) = Т₂ -Т₁,

де (j₁ - j₂) - прискорююча різниця потенціалів (або прискорююча напруга  U) ; Т₁ і Т₂ - початкова і кінцева кінетичні енергії протона.

Нехтуючи початковою кінетичною енергією (Т₁ » 0) і виражаючи кінетичну енергію Т₂ через імпульс  Р, одержимо

QU =.

Знайдемо з цього виразу імпульс  і підставимо його в формулу (3)

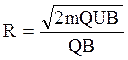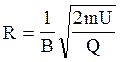 або .     (4)

Переконємось в тому, що права частина рівності дає одиницю довжини (м):

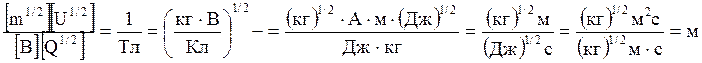
Підставимо в формулу (4) числові значення фізичних величин і виконаємо обчислення

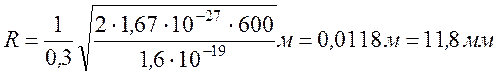
          Приклад 7. Електрон, влетівши в однорідне магнітне поле (В = 0,2 Тл), став рухатися по колу радіусом R= 5 см. Визначити магнітний момент Р еквівалентного кругового струму.

Розв’язання

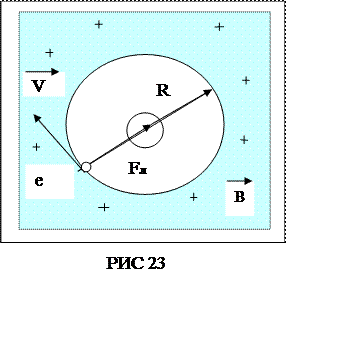          Електрон починає рухатися по колу, якщо він влітає в однорідне магнітне поле перпендикулярно лініям магнітної індукції. На рис. 23 лінії магнітної індукції перпендикулярні площині рисунка і направлені «від нас» (позначені хрестиками).

Рух електрона по колу еквівалентний круговому струму, який в даному випадку визначається виразом                                                   

І_екв=,

де е  - заряд електрона;

Т - період його обертання.

Період обертання можна виразити через швидкість електрона V і шлях, який проходить електрон за період,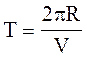

Тоді                                               І_екв =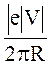                    (1)

         Знаючи  І_екв, знайдемо магнітний момент еквівалентного кругового струму. Магнітний момент контура із струмом виражається співвідношенням

                                                Р_m = I_екв  . S ,               (2)

де S - площа, обмежена колом, описаним електроном ( S = pR²)

Підставивши І_екв з (1) в вираз (2), одержимо

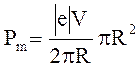
Скоротимо на pR і перепишемо цей вираз в вигляді

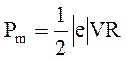                            (3)

В одержаному виразі відомою  є швидкість електрона, яка зв’язана з радіусом R кола, по якому він рухається, співвідношенням

R =      (див.приклад 6).

Замінивши Q на , знайдемо  швидкість 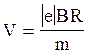і підставимо її в формулу (3):

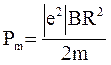                               (4)

Переконавшись в тому, що права частина рівняння (4) дає одиницю магнітного моменту ( А . м²)

,

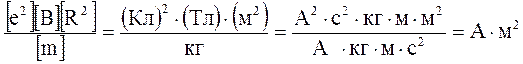виконаємо обчислення

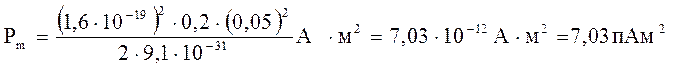
          Приклад 8. Альфа-частинка пройшла прискорюючу різницю потенціалів U=104 В і влетіла в схрещені під прямим кутом електричне (Е=10 кВ/м) і магнітне  (В = 0,1 Тл) поля.

Знайти відношення заряду альфа-частинки до її маси, якщо рухаючись перпендикулярно до обох полів, частинка не відхиляється від прямолінійної траєкторії.

                                                  Розв’язання

          Для того, щоб знайти відношення заряду Q альфа-частинки до її маси m , скористуємось зв’язком між роботою сил електричного поля і зміною кінетичної енергії частинки:

QU =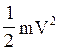,                      звідки  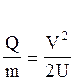                                                (1)

Швидкість V альфа -частинки знайдемо з наступних міркувань. В схрещених електричному і магнітному полях на рухому заряджену частинку діють дві сили:

сила Лоренца   , направлена перпендикулярно швидкості  і вектору магнітної індукції  , і кулонівська сила  , співнаправлена з вектором напруженості  електростатичного поля (Q>0).

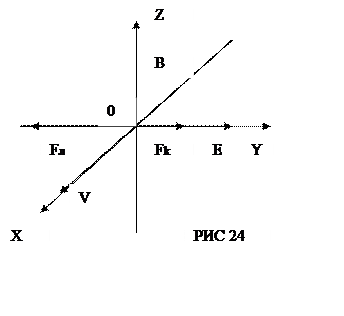
 На рис.24 направимо вектор магнітної індукції  В  уздовж осі  OZ, швидкість   - позитивному напрямку осі  Ох , тоді   ….і будуть направлені так, як показано на рисунку.

Альфа - частинка не буде відчувати відхилення, якщо геометрична сумма сил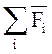буде дорівнювати нулю. В проекції на вісь Оy одержимо наступну  рівність (при цьому враховано, що і sin a= 1)

QE - QVB = 0

Звідки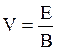                                             

Підставивши цей вираз швидкості в формулу (1), одержимо

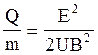
Переконаємось в тому, що права частина рівності дає одиницю питомого заряду (Кл/кг):

                              

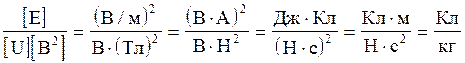
Виконаємо обчислення

                               

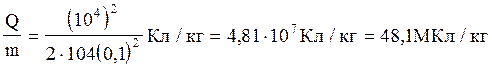
          Приклад 9. Коротка котушка, яка вміщує N = 10³ витків, рівномірно обертається з частотою  n = 10 с^-1 відносно осі АВ, яка лежить в площині котушки і перпендикулярна лініям однорідного магнітного поля ( В = 0,04 Тл). Визначити миттєве значення Е.Р.С. індукції для тих моментів часу, коли площина котушки утворює кут a = 60^о з лініями поля. Площа  S котушки дорівнює 100 см².

                                                        Розв’язання

Миттєве значення Е.Р.С. індукції e_і визначається рівнянням електромагнітної індукції Фарадея-Максвелла

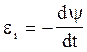            (1)

Потокозчеплення      y = NФ,  де N - кількість витків котушки, які пронизані магнітним потоком Ф.

Підставивши вираз Y в формулу (1), одержимо

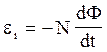      (2)

При обертанні котушки магнітний потік Ф, який пронизує котушку в момент часу t, змінюється по  закону Ф = Bscos wt, де В - магнітна індукція;  S - площа котушки; w - кутова швидкість котушки. Підставивши в формулу (2) вираз магнітного потоку Ф і взявши першу похідну за часом, знайдемо миттєве значення Е.Р.С. індукції:

e_і = NBSw . sinwt

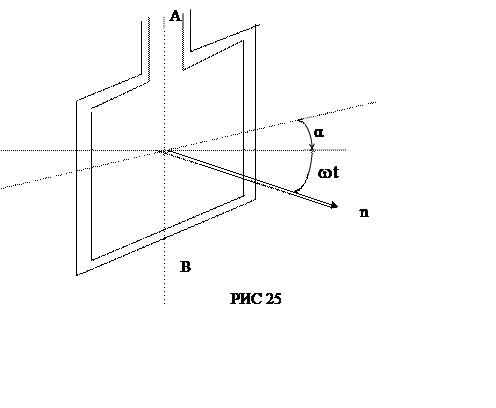
Помітивши, що кутова швидкість w зв’язана з частотою обертання n котушки співвідношенням  w= 2pn і що кут wt =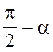 (рис.25), одержимо (враховано, що

sin (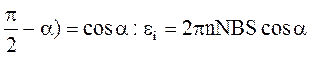

Переконаємось в тому, що права частина цієї рівності дає одиницю Е.Р.С. (В):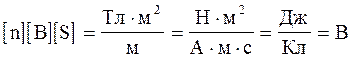

Виконаємо обчислення

e = 2 . 3,14 . 10 . 10³ . 0,04 . 10^-2 . 0,5В = 25,1 В

          Приклад 10. Квадратна дротяна рамка, сторона якої  а = 5 см, і опором   R= 10 Ом знаходиться в однорідному магнітному полі (В = 40 Тл). Нормаль до площини рамки утворює кут a = 30^о з лініями магнітної індукції. Визначити заряд Q, який пройде по рамці, якщо магнітне поле виключити.