Экономика и менеджмент \ Статистика

Изучение потребительского поведения, страница 3


Приложение 4

Расчет показателей вариации

1)  Коэффициент вариации долей.

Служит количественной оценкой состава ответов, выраженных качественными признаками. Расчет данного показателя осуществляется по следующей формуле:

*       ;

где к – число групп в совокупности;

di – доля i-группы в совокупности.

Рассмотрим расчет коэффициента вариации долей на примере распределения респондентов по полу. В зависимости от пола всех респондентов можно разделить на 2 группы: мужчины и женщины. В нашем примере доля мужчин в общей численности опрошенных составила 48%, а доля женщин 52%. Подставляя полученные значения в формулу, получаем:

Данный показатель характеризует однородность распределения единиц в совокупности. В нашем примере значение показателя меньше 0.3, что позволяет сделать вывод  о том, что распределение респондентов по полу отличается высокой однородностью.

2)  Коэффициенты вариации.

Данный показатель характеризует однородность распределения единиц в совокупности по количественному признаку. Расчет производится по формуле:

;

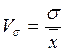Рассмотрим расчет данного показателя на примере распределения респондентов по возрасту.

Дисперсия рассчитывается по следующей формуле:

;

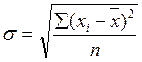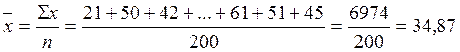
Таким образом, средний возраст респондента составляет 34, 87 лет.

3) Дисперсия альтернативного признака.

Рассчитывается по формуле:

;

где n – доля респондентов в 1 группе.

Рассчитаем дисперсию альтернативного признака ответов на вопрос: «При выборе конкретного товара, подвержены ли вы влиянию со стороны семьи, друзей, соседей, коллег по работе и проч.?» Предлагались следующие мнения:

а) да, подвержены;

б) нет, придерживаюсь только собственного мнения.

Продолжение приложения 4

4) Расчет коэффициента вариации для ранжируемых объектов

Формула коэффициента вариации для ранжируемых объектов выглядит следующим образом:

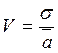
Расчет среднеквадратического отклонения производится по следующей формуле:

;

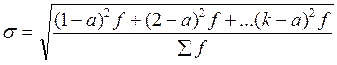где f – число респондентов, поставивших ранжируемый объект на к-тое место.

Таким образом, среднеквадратическое отклонение для первого объекта будет выглядеть следующим образом:

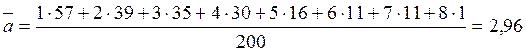
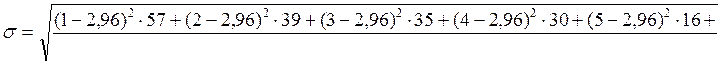
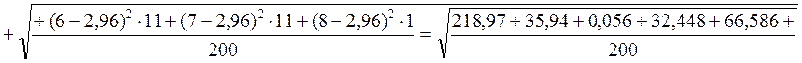
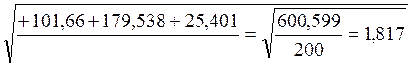
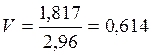
Далее расчет проводится аналогично.


 Приложение 5

Изучение потребительских предпочтений

Средний балл

Ранги

d2

мужчины

женщины

Rx

Ry

Одежда

2.90

3.01

1

2

1

Бытовая химия

3.95

2.90

3

1

4

Косметика, парфюмерия

5.49

3.04

7

3

16

Лекарственные средства

4.64

4.29

5

4

1

Бытовая техника

4.47

6.23

4

7

9

Канцелярские товары

4.99

4.99

6

6

0

Печатные издания

3.52

4.87

2

5

9

Ювелирные изделия

6.55

7.17

8

8

0

Произведения искусства

8.07

8.54

9

9

0

Итого

40

Формула коэффициента корреляции рангов Спирмэна имеет вид:

                        ;

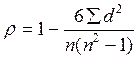где d – разность рангов признаков x и у;

n – число ранжируемых объектов.

Помимо оценки тесноты связи при качественной информации коэффициент корреляции рангов может выступать оценкой единодушия общественного мнения. Чем ближе по абсолютной величине рассчитанный показатель к1, тем степень единодушия мнения больше.

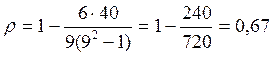
Далее необходимо оценить рассчитанный коэффициент на статистическую значимость.

При n£30  значимость рангового коэффициента Спирмэна определяется по специальной таблице значений коэффициента корреляции рангов Спирмэна для двусторонних пределов уровня значимости a.

Для рассчитанного нами рангового коэффициента корреляции Спирмэна его предельное значение при 9 ранжируемых единицах и уровне значимости a=0,05 составляет 0,6833, что больше рассчитанного r=0,67. Таким образом, мы можем прийти к выводу о значительных разногласиях во мнениях респондентов.


Приложение 6

Построение уравнения регрессии и расчет линейного коэффициента корреляции между потребительскими доходами и расходами

Regression Analysis - Linear model: Y = a + b*X

-----------------------------------------------------------------------------

Dependent variable: Y

Independent variable: X

-----------------------------------------------------------------------------

                               Standard          T

Parameter       Estimate         Error       Statistic        P-Value

-----------------------------------------------------------------------------

Intercept        66,6439        76,5608        2,87047         0,0094

Slope           0,853408      0,0141796        60,1856         0,0000

-----------------------------------------------------------------------------

                           Analysis of Variance

-----------------------------------------------------------------------------

Source             Sum of Squares     Df  Mean Square    F-Ratio      P-Value

-----------------------------------------------------------------------------

Model                   6,60826E7      1    6,60826E7    3622,31       0,0000

Residual                 145946,0      8      18243,2

-----------------------------------------------------------------------------

Total (Corr.)           6,62286E7      9

Correlation Coefficient = 0,998898

R-squared = 99,7796 percent

Standard Error of Est. = 135,068

Скачать файл