


С железнодорожного вокзала можно отправлять ежедневно скорые и курьерские поезда. Вместимость вагонов и наличный парк на станции указан в таблице.
|
Тип вагонов |
Багажные |
Почтовые |
Жесткие |
Купейные |
Мягкие |
Вид поезда |
|
Число вагонов в поезде |
1 |
-- |
5 |
6 |
3 |
курьерский |
|
1 |
1 |
8 |
4 |
1 |
скорый |
|
|
Вместимость |
-- |
-- |
58 |
40 |
32 |
|
|
Парк |
12 |
8 |
81 |
70 |
27 |
Найти соотношение между количеством скорых и курьерских поездов, чтобы число пассажиров, которых можно отправить ежедневно достигло максимума.
Решение:
Пусть х1 - число курьерских поездов;
х2 - число скорых поездов;
Строим область допустимых значений. Областью решений линейного неравенства с двумя переменными является полуплоскость лежащая по одну сторону от граничной прямой, уравнение которой можно получить, если заменить знак неравенства на знак равенства.
Ограничения:
![]()
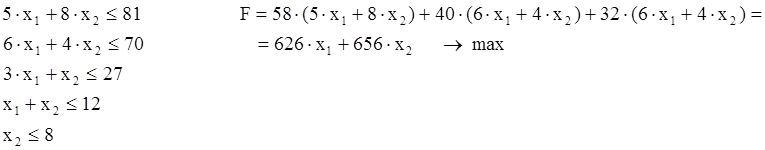
626×x1 + 656×x2 = 0
Функция F имеет оптимум в точках А, В или С. Определим точку минимума с помощью основной теоремы линейного программирования.
Строим F=0, затем строим градиент grad F.
Двигая линию уровня в направлении градиента определим точки области значений с которой соприкасается линия уровня – эта точка и определит координату оптимального решения.
Решением является точка А с координатами х1=5, х2=7.
Fmax = 7722.
Решим поставленную задачу симплекс-методом.
Дополним неравенство до равенства
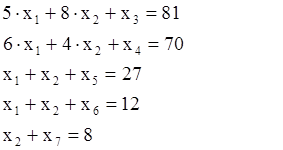
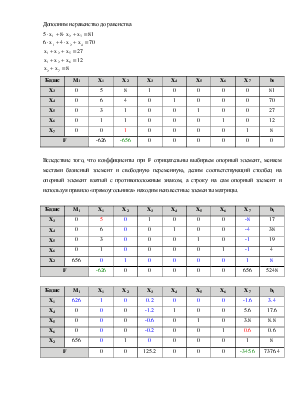
|
Базис |
Mi |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
bi |
|
X3 |
0 |
5 |
8 |
1 |
0 |
0 |
0 |
0 |
81 |
|
X4 |
0 |
6 |
4 |
0 |
1 |
0 |
0 |
0 |
70 |
|
X5 |
0 |
3 |
1 |
0 |
0 |
1 |
0 |
0 |
27 |
|
X6 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
12 |
|
X7 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
8 |
F |
-626 |
-656 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Вследствие того, что коэффициенты при F отрицательны выбираем опорный элемент, меняем местами базисный элемент и свободную переменную, делим соответствующий столбец на опорный элемент взятый с противоположным знаком, а строку на сам опорный элемент и используя правило «прямоугольника» находим неизвестные элементы матрицы.
|
Базис |
Mi |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
bi |
|
X3 |
0 |
5 |
0 |
1 |
0 |
0 |
0 |
-8 |
17 |
|
X4 |
0 |
6 |
0 |
0 |
1 |
0 |
0 |
-4 |
38 |
|
X5 |
0 |
3 |
0 |
0 |
0 |
1 |
0 |
-1 |
19 |
|
X6 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
-1 |
4 |
|
X2 |
656 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
8 |
F |
-626 |
0 |
0 |
0 |
0 |
0 |
656 |
5248 |
|
|
Базис |
Mi |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
bi |
|
X1 |
626 |
1 |
0 |
0.2 |
0 |
0 |
0 |
-1.6 |
3.4 |
|
X4 |
0 |
0 |
0 |
-1.2 |
1 |
0 |
0 |
5.6 |
17.6 |
|
X5 |
0 |
0 |
0 |
-0.6 |
0 |
1 |
0 |
3.8 |
8.8 |
|
X6 |
0 |
0 |
0 |
-0.2 |
0 |
0 |
1 |
0.6 |
0.6 |
|
X2 |
656 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
8 |
F |
0 |
0 |
125.2 |
0 |
0 |
0 |
-345.6 |
7376.4 |
|
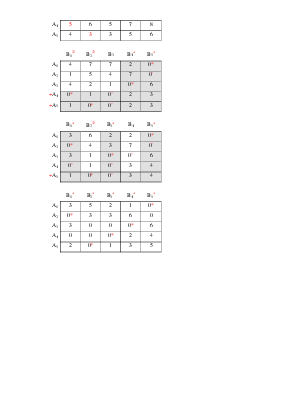
|
Базис |
Mi |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
bi |
|
X1 |
626 |
0 |
5 |
||||||
|
X4 |
0 |
0 |
12 |
||||||
|
X5 |
0 |
0 |
5 |
||||||
|
X7 |
0 |
0 |
0 |
-1/3 |
0 |
0 |
5/3 |
1 |
1 |
|
X2 |
656 |
0 |
7 |
||||||
F |
0 |
0 |
10 |
0 |
0 |
576 |
0 |
7722 |
|
Получаем решение: Число перевозимых пассажиров будет максимально (7722 чел.), если с железнодорожного вокзала ежедневно отправлять 5 курьерских и 7 скорых поездов. При этом невостребованными останутся 12 купейных, 5 мягких и 1 почтовый вагон.
Двойственная задача.
Математическая модель двойственной задачи подчиняется следующим правилам:
Ø Количество двойственных переменных равно количеству ограничений в исходной задаче;
Ø Fmax ® Zmin и наоборот;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.