Определение соотношения между количеством скорых и курьерских поездов, страница 2

Ø  Свободные члены ограниченные прямой задачей служат коэффициентами целевой двойственной функции, а коэффициенты прямой – ограничениями двойственной;

Ø  Матрица коэффициентов А двойственной задачи есть А^Т прямой задачи;

Поэтому: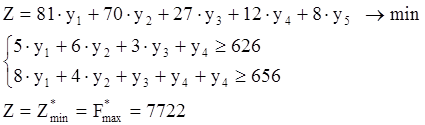   

Аналогично предыдущему пункту получаем искомое решение:

Двойственные оценки:

Y₂, Y₃, Y₅ – не являются дефицитными;

Y₁, Y₄ - являются дефицитными;

Т.о., при увеличении наличного парка вагонов на 1 жесткий вагон произойдет увеличение F на 10 ед., а при увеличении багажных вагонов на 1 – F возрастет на 576 ед.

Задача №2  Транспортная задача.

Задача задана следующей матрицей величины C_ij – стоимостей перевозки от поставщика A_i (i=1, 2, 3) к получателю B_ij (j=1, 2, 3, 4).

Начальный план перевозок будем составлять методом наименьших стоимостей. Максимально возможные перевозки в тех клетках матрицы, для которых транспортные издержки C_ij минимальны.

Проверим начальный план на оптимальность методом потенциалов:

V₂ - U₃ = 29 – 28 = 1

Допустим Z > 6 неоптимальный план.

Наибольшее значение C_ij = 4, принимаем U₃ = 28.

Для клеток должны выполнятся следующие равенства:

V₁ - U₃ = C₃₁ ; V₁= C₃₁ + U₃ = 32 ;

V₃ - U₃ = C₃₃ ; V₃= C₃₃ + U₃ = 30 ;

V₁ - U₃ = C₁₁ ; U₁= -C₁₁+ V₃ = 30 ;

V₃ – U₂ = C₂₃ ; U₂= -C₂₃ + V₃ = 29 ;

V₂ – U₂ = C₂₂ ; V₂= C₂₂ + U₂ = 31 ;

V₄ - U₃ = C₄₃ ; V₁= C₄₃ + U₃ = 31 ;

Проверим условия   V_j – U_i £ C_ij    для   x_ij=0.

V₂ – U₁ = 1 < 8            V₁ – U₂ = 3 = 3

V₃ – U₁ = 0 < 6            V₄ – U₂ = 3 <  5

V₄ – U₁ = 1 < 6            V₂ – U₃ = 3 <  6

Отсюда следует, что полученный план является оптимальным. Значение целевой функции для оптимального плана:

Задача №2 Задача о назначениях.