Конические зубчатые передачи. Геометрия зацепления. Эквивалентные и биэквивалентные параметры

Лекция №15

Тема 15: Конические зубчатые передачи

15.1. Общие сведения

Конические колёса применяют для передачи вращения между пересекающимися осями. Межосевой угол S может быть в диапазоне 10^° < S < 170^°. Наиболее распространены ортогональные передачи с углом S = 90^°.

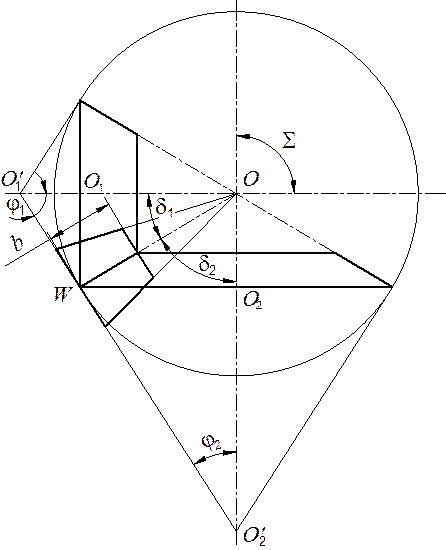Коническая передача является пространственной сферической передачей (рис. 15.1). В плоскости осей 1 и 2 всегда можно найти такую точку W, скорости которой будут одинаковыми как при движении с шестерней, так и при движении с колесом. Положение этой точки определяется передаточным отношением . Также это справедливо для любой точки прямой OW, расположенной к осям колёс под углами  и , которая является мгновенной осью вращения.

Рис. 15.1. Коническая передача

Вращая  OW относительно обеих осей, получают  начальные конусы, перекатывающиеся друг по другу без скольжения, по аналогии с начальными цилиндрами в цилиндрической передаче. Для ограничения размеров начальные конусы пересекаются сферой радиусом OW. В сечениях получаются окружности с центрами O₁и O₂ и начальными радиусами O₁Wи O₂W. Передаточное число:

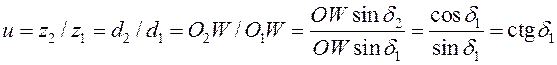,    (15.1)

откуда начальные углы при вершинах конусов шестерни и колеса:

;                                     (15.2)

.                                             (15.3)

В конических передачах используются усечённые начальные конусы шириной b. В коническом зацеплении линия OW – общая образующая начальных конусов. Конические передачи изготавливают обычно с суммарным смещением x_Σ= 0, поэтому начальные конусы совпадают с делительными. Зубья конических колёс располагаются около начальных конусов. Поперечные сечения зубьев постепенно уменьшаются в направлении вершин.

Торцы зубьев имеют сферическую поверхность, которая на плоскость не развёртывается. Замена сферической поверхности поверхностями дополнительных конусов образует профиль, незначительно отличающийся от эвольвентного, но упрощает профилирование, так как поверхность конуса можно развернуть на плоскость. Образующие дополнительных конусов проводят перпендикулярно мгновенной оси вращения OW.  Углы при вершинах дополнительных конусов .

Дополнительные конусы формируют торцы конических колёс – наружный, которому присваивают индекс е, и внутренний – i. Расчётным является среднее сечение – индекс m. Большинство измерений выполняют по наружному торцу, так как это более удобно.

Профиль конического зуба получается при обкатывании производящей плоскости по основному конусу аналогично обкатыванию по цилиндру. При этом на поверхности дополнительных конусов получается профиль, близкий к эвольвентному. Коническое зацепление происходит аналогично цилиндрическому (рис. 15.2). Плоскость зацепления B₁WB₂ проходит через полюс W по касательной к основным конусам и располагается под углом зацепления  к касательной к начальным конусам.

Рис.15.2. Плоскость зацепления

15.2. Геометрия зацепления

Конические прямозубые колеса нарезают на зуборезных станках инструментами с параметрами исходного контура по ГОСТ 13754 (; ; ). На рис. 15.3 показано нарезание прямозубых колёс, где резцы при нарезании впадины перемещаются под углом друг к другу. При этом зуб нарезаемого колеса будет иметь переменную высоту в связи с разной глубиной захода резцов. В крупносерийном и массовом производстве зубья нарезают резцовой головкой (рис. 15.4). В большинстве случаев инструмент при обработке обкатывается по делительному конусу, совпадающему с начальным конусом колеса. В соответствии с известной зависимостью

                                                        (15.4)

при изменении диаметров должны меняться модули зацепления, так как для конкретного колеса . В расчётах используют внешний модуль  и

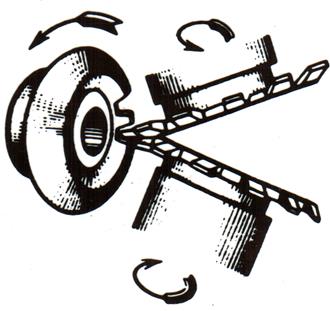
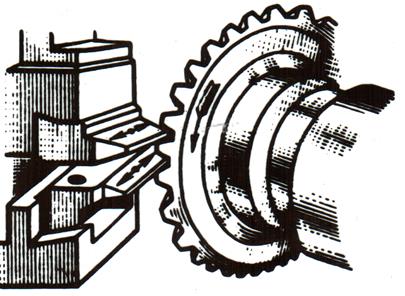
     Рис. 15.3. Зубонарезание резцами           Рис. 15.4. Нарезание резцовой головкой

средний модуль . Через внешний модуль определяют внешний делительный диаметр

,                                                     (15.5)

который, как и большинство диаметров, определяют по наружному торцу (рис. 15.5). Средний делительный диаметр определяют на среднем сечении, расположенном перпендикулярно образующей начальных конусов на расстоянии b/2 от торцов:

.                                                     (15.6)

Внешний модуль  может иметь нестандартное значение (определяемое с точностью до сотых долей мм) либо округляется до стандартного значения по ГОСТ 9563 при сохранении стандартным внешнего делительного диаметра колеса d_e2.

На чертеже передачи (рис. 15.5) изображены диаметры  и , межосевой угол S, углы при вершинах конусов  и , ширина венца b, половина ширины венца b/2, радиальный зазор c, высота головки h_aeи ножки h_fе  зуба.

Важнейшим размером конической передачи является внешнее конусное расстояние , которое по смыслу подобно межосевому расстоянию  в цилиндрической передаче. Внешнее конусное расстояние определяют как расстояние от вершин конусов до внешнего торца. Величину  находят из прямоугольного треугольника:

                                             (15.7)

или из теоремы Пифагора:

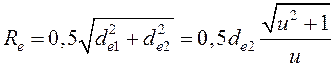.                                (15.8)

Рис. 15.5. Коническое зацепление

Аналогично по формуле (15.7) определяют среднее конусное расстояние – расстояние от вершины до среднего сечения:

.                                          (15.9)

Соотношение между модулями устанавливается из простой зависимости:

,                                           (15.10)

с учетом формул (15.7) и (15.9):

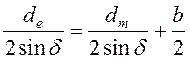.                                     (15.11)

Подставляя  и  из формул (15.5) и (15.6) в формулу (15.11) и умножая обе части на , получают:

.                                      (15.12)