Конические зубчатые передачи. Геометрия зацепления. Эквивалентные и биэквивалентные параметры, страница 2

Высота зубьев зависит от принятой формы; например, форма 1 предполагает пропорциональное понижение зуба и впадины. Для этой формы диаметры вершин и впадин по внешнему торцу определяют через делительные диаметры и проекции высоты головки или ножки зуба на направление измерений:

;                         (15.13)

.                                    (15.14)

Углы головок и ножек находятся из тригонометрических соотношений:

;                                   (15.15)

.                                       (15.16)

Углы конусов вершин и впадин:

;                                             (15.17)

.                                            (15.18)

Ширину зубчатого венца принимают по соотношению:

.                                     (15.19)

Наряду с прямозубыми передачами применяют косозубые и с круговым зубом (рис. 15.6).

 

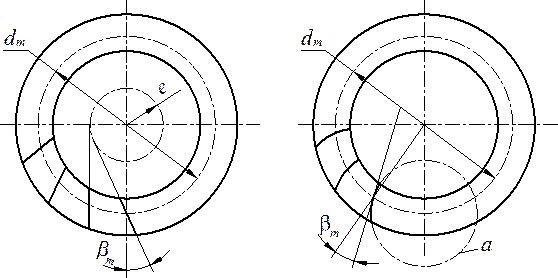Рис. 15.6. Непрямозубые конические колёса

За расчётный угол наклона принимают угол на средней окружности между касательной и образующей конуса в данной точке. Обычно принимают углы  для колёс с тангенциальными зубьями и  для колёс с круговыми зубьями. В непрямозубых колёсах в расчётных формулах появляется нормальное сечение со средним нормальным модулем , а и становятся окружными модулями:  – внешний окружной модуль,  – средний окружной модуль.

15.3. Эквивалентные и биэквивалентные параметры

Параметры эквивалентных колёс используют при расчётах на прочность. Форма профиля зуба конического колеса в нормальном сечении дополнительным конусом эквивалентна профилю цилиндрического прямозубого колеса. Эквивалентное цилиндрическое колесо получается как развёртка дополнительного конуса на плоскость (рис. 15.7). Эквивалентный диаметр:

.                                          (15.20)

На колесе большего размера можно нарезать большее число зубьев. Эквивалентное число зубьев:

.                                        (15.21)

 

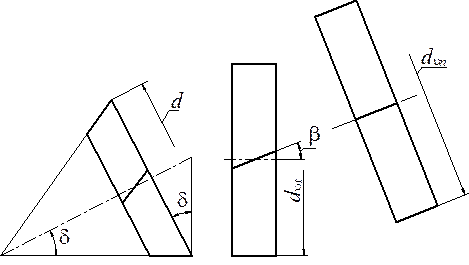Рис. 15.7. Эквивалентное и биэквивалентное колёса

Из формул (15.20) и (15.21) следует, что эквивалентные параметры выше действительных. Однако нагрузочная способность конических колес не выше цилиндрических по ряду причин:

1) для нарезания конических колес требуются специальные станки и специальные инструменты;

2) при изготовлении требуется выдержать допуски не только на линейные размеры, но и на углы  и др.;

3) при монтаже необходимо обеспечить совпадение вершин начальных конусов;

4) выполнить коническое зацепление с той же степенью точности, что и цилиндрическое, значительно труднее;

5) пересечение осей затрудняет размещение валов, поэтому колёса располагают несимметрично и консольно относительно опор;

6) наличие осевых сил усложняет конструкцию опор.

Всё это приводит к тому, что нагрузочная способность прямозубой конической передачи составляет лишь 0,85 цилиндрической (на основании опытных данных). При этом сохраняются преимущества передачи с непрямыми зубьями по сравнению с прямозубой передачей. Это выражается биэквивалентными параметрами, получающимися в результате двойного приведения: конической к цилиндрической и косозубой к прямозубой передаче. Используя зависимости для цилиндрических косозубых колес (п. 14.2) и формулы (15.20) и (15.21), можно записать:

биэквивалентный диаметр ;                                   (15.22)

биэквивалентное число зубьев  .                            (15.23)

Несмотря на сложность изготовления и монтажа конические передачи получили широкое распространение в редукторостроении, автотракторной и авиационной промышленности.

15.4. Силы в зацеплении

Нормальную силу в коническом зацеплении  раскладывают на три составляющие (рис. 15.8). Окружная сила:

.                                                (15.24)

Силу раскладывают по двум направлениям: радиальное усилие на шестерне , равное осевому на колесе: