Конические зубчатые передачи. Геометрия зацепления. Эквивалентные и биэквивалентные параметры, страница 3

                     (15.25)

и осевое усилие на шестерне, равное радиальному на колесе:

.                                (15.26)

Нормальная сила:

.                                      (15.27)

Приведенные формулы относятся к прямозубому зацеплению. Для не-прямозубых колёс формулы расчёта усилий приведены в учебнике [6].

 

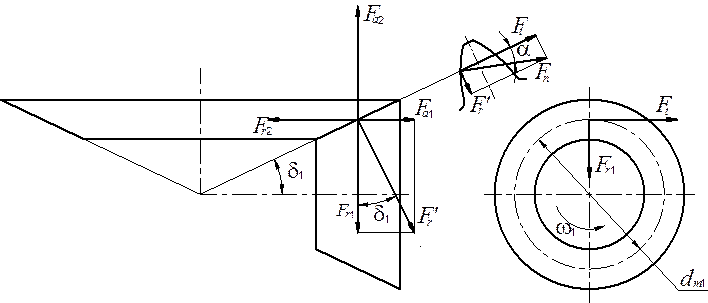Рис. 15.8. Силы в конической передаче

15.5. Особенности расчётов на прочность

А) Контактная прочность. Расчёт ведут по формуле Герца:

.

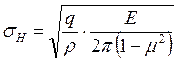Приведенный радиус кривизны определяют по средним диаметрам эквивалентных колёс:

.

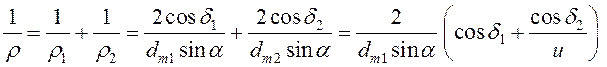Учитывая связь тригонометрических функций, находят:

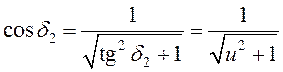;                               (15.28)

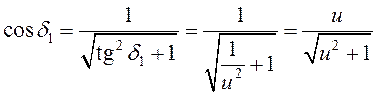.                    (15.29)

После подстановки и преобразований:

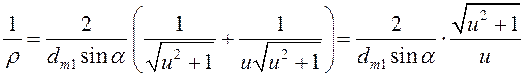.    (15.30)

После преобразований формула Герца примет вид, аналогичный формуле (14.33) для цилиндрических зубчатых передач:

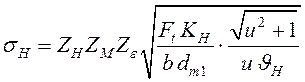,                       (15.31)

где  – опытный коэффициент; для прямозубых передач = 0,85; для непрямозубых колес его определяют по эмпирическим формулам [11]; в среднем нагрузочная способность передач с круговыми зубьями в 1,4…1,5 раза выше прямозубых. После подстановки численных данных и упрощений формула (15.31) примет форму, удобную для проверочного расчёта:

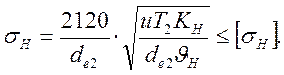                                      (15.32)

Для проектного расчёта формулу (15.32) решают относительно :

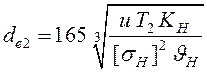.                                      (15.33)

Величину  округляют до стандартной по ГОСТ 12289 или по ГОСТ 6636 (прил. 15).

Б) Изгибная прочность. Расчёт ведут по формуле, соответствующей цилиндрической передаче:

s_F1 = Y_F1F_tK_FbK_Fn/(_F·bm_m) ≤[s_F] ,                                (15.34)

где  – коэффициент, учитывающий особенности передач; для прямо-зубых колес = 0,85; для непрямозубых определяют по [9];

     – коэффициент формы зуба, определяемый по биэквивалентному числу зубьев.

Пример 15.1. Рассчитать прямозубую коническую зубчатую передачу по следующим исходным данным: мощности на валах: Р₁ = 7 кВт, Р₂ = 6,65 кВт, частоты вращения валов: n₁ = 480 об/мин, n₂ = 152 об/мин. Недостающими данными задаться.

Решение.

Вычерчиваем кинематическую схему передачи (рис. 15. 9).

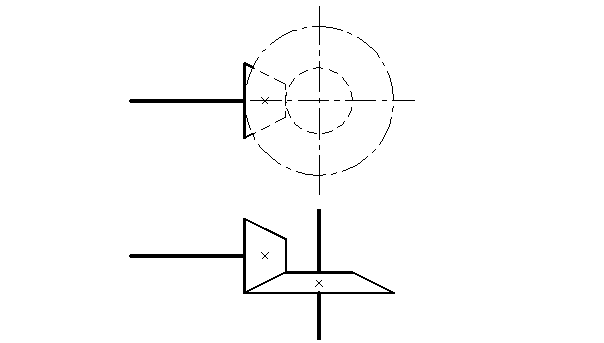
Рис. 15. 9. Кинематическая схема конической передачи

            Принимаем материал шестерни сталь 30ХГС, термообработка – закалка, твёрдость 45…55HRC, колеса – сталь 40ХН, термообработка – улучшение, средняя твёрдость 250HB[9]. Допускаемые контактные напряжения шестерни и колеса принимаем по примеру 14.1:  = 627 МПа,  

Крутящий момент на валу колеса: Т₂ = 9550·6,65/152 = 417,8 Н·м.

Передаточное число u = 480/152 = 3,16.

Принимаем 7-ю степень точности изготовления колёс. Коэффициенты нагрузки принимаем по 8-й степени точности для цилиндрических колёс: концентрации нагрузки  = 1,3;  динамической нагрузки = 1,05. Внешний делительный диаметр колеса из расчёта на контактную выносливость:

  

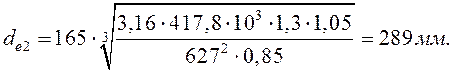
Принимаем  = 290 мм по ГОСТ 6636. Принимаем   (рекомендуется ).Число зубьев колеса   Внешний окружной модуль

Углы при вершинах делительных конусов шестерни и колеса:

;

Внешний делительный диаметр шестерни:

Внешнее конусное расстояние:

Ширина венцов b = K_beR_e = 0,285·152,09 = 43,3 мм. Принимаем  по ГОСТ 6636.

Среднее конусное расстояние:

Средний модуль:

Средние делительные диаметры:

Диаметры вершин:       

          

Диаметры впадин:

      

Углы головок и ножек для формы 1:

 

Углы конусов вершин и впадин:

                             

Окружная скорость колёс u =pd_m1n₁/60000 = π·78,25·480/60000 = 1,97 м/с.

Уточняем коэффициенты нагрузки для 8-й степени точности: = 1,24; = 1,05. Коэффициент   = 0,85. Рабочее контактное напряжение:

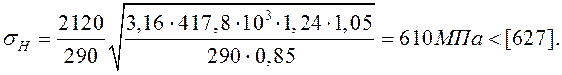
Вывод. Контактная прочность достаточна.

Окружное усилие в зацеплении:

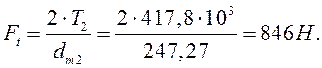
Радиальное усилие F_r1 = F_a2 = F_t·tga·cos= 846·tg20º·cos17,56º = 276 Н.

Осевое усилие F_a1 = F_r2 = F_t·tga·sin = 846·tg20 º·sin 17,56º = 93 Н.