Standard Error of Est. = 0,18409
Mean absolute error = 0,0690247
Durbin-Watson statistic = 2,87495
Рисунок 4.2.2 Предварительные результаты построения модели
Щелкнем правой кнопкой мыши, появится меню, в котором нужно выбрать AnalysisOptions (Опции анализа) для вызова пошаговой регрессии.
Процедура пошаговой регрессии дает возможность автоматического подбора адекватной модели. При этом используются два основных подхода: ForwardSelection(Включения факторов) или Backward Selection(Исключения Факторов) (рисунок 4.2.3.).
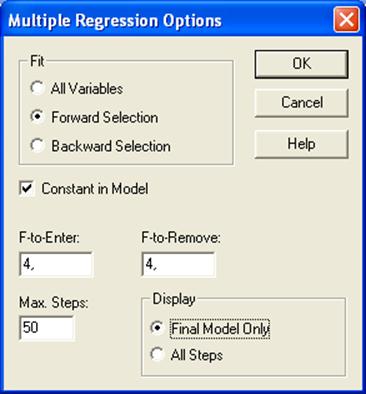
Fit – Подбирать; AllVariable – Все переменные; ForwardSelection -Включение факторов; Backward Selection- Исключение Факторов; ConstantinModel - Свободный член модели; F-to-Enter – Включение; F-to-Remove – Исключение; MaxSteps – Максимальное число шагов; Display – Показать;FinalModelOnly– Только заключительная модель; AllSteps– Все шаги.
Рисунок 4.2.3. – Окно MultipleRegressionOption (Опции множественной регрессии). Модель пошаговой регрессии
Флажок в поле ConstantinModel (Свободный член модели) предполагает наличие в модели свободного члена. Установлено также , что F-критерий для включения (F-to-Enter) и исключения (F-to-Remove) независимых переменных равен 4. Максимальное количество шагов при построении модели (Max Steps) - 50. Флажок в поле All Steps (Все шаги) требует вывод на экран всех промежуточных этапов построения уравнения регрессии.
Отметив поле ForwardSelection(Включения факторов) и FinalModelOnlyполучим результаты заключительной модели (промежуточные этапы построения модели не показаны) (рисунок 4.2.4.).
Multiple Regression Analysis
-----------------------------------------------------------------------------
Dependent variable: Y
-----------------------------------------------------------------------------
Standard T
Parameter Estimate Error Statistic P-Value
-----------------------------------------------------------------------------
CONSTANT 9,99392 0,954915 10,4658 0,0000
X10 0,155791 0,035976 4,33043 0,0019
X2 3,80885 1,02886 3,702 0,0049
X3 0,119721 0,0125751 9,52045 0,0000
X4 0,0685042 0,0250069 2,73941 0,0229
-----------------------------------------------------------------------------
Analysis of Variance
-----------------------------------------------------------------------------
Source Sum of Squares Df Mean Square F-Ratio P-Value
-----------------------------------------------------------------------------
Model 27,2717 4 6,81792 252,92 0,0000
Residual 0,242607 9 0,0269563
-----------------------------------------------------------------------------
Total (Corr.) 27,5143 13
R-squared = 99,1183 percent
R-squared (adjusted for d.f.) = 98,7264 percent
Standard Error of Est. = 0,164184
Mean absolute error = 0,0978855
Durbin-Watson statistic = 2,02579
Stepwise regression
-------------------
Method: forward selection
F-to-enter: 4,0
F-to-remove: 4,0
Final model selected
Рисунок 4.2.4. Окончательные результаты выбора модели
Основные результаты расчета сведены в две таблицы: в первой отражены результаты регрессионного анализа, во второй представлен дисперсионный анализ. Внизу показана дополнительная информация: R-squared – коэффициент детерминации; R-squared (adjustedford.f.) - коэффициент детерминации, приведенный с учетом степеней свободы; StandardErrorofEst. (SE) – стандартная ошибка оценивания; Meanabsoluteerror–стандартная ошибка оценивания; Durbin-Watsonstatistic– статистика Дарбина-Уотсона.
На основе частных F-критериев из 10 независимых переменных в модель средней обеспеченности населения жильём всего кв. м общей площади на одного жителя включены 4 фактора: средняя стоимость строительства за 1 кв.м., руб (в сопоставимых ценах) (Х2); денежные доходы в расчете на душу населения в среднем за месяц, тыс.руб. (в сопоставимых ценах) (Х3); удельный вес частного жилого фонда, % (Х4); ввод в действие жилых домов, тыс. кв. метров общей площади; (Х10). Построена следующая модель:
Y=9,99392 + 3,80885*X2 + 0,119721*X3 + 0,0685042*X4+ 0,155791*X10
Все отобранные факторы статистически значимы, так как фактический t-критерий Стьюдента больше табличного (приложение В). Об этом свидетельствует графа 5 таблицы рисунка 4.2.4. (P-Value), в которой отражены вероятности наиболее существенных факторов динамики средней обеспеченности населения жильём.
Дисперсионный анализ (AnalysisofVariance) позволяет получить F-критерий для оценки адекватности модели. Представленные на рисунке 4.2.4. данные свидетельствуют о хорошей адекватности модели . Фактический критерий Фишера (F-Ratio), равный 252,92, в 69,7 раза больше табличного значения. Стандартная ошибка остатков (Standard Error of Est.) составляет 0,164184. Приведенный с учетом степеней свободы коэффициент детерминации (R-squared (adjusted for d.f.) равный 98,7264% свидетельствует о том, что вариация средней обеспеченности населения жильём на 98,7% обусловлена включенными в модель факторами. Статистика Дарбина–Уотсона (Durbin-Watson statistic), составляющая 2,02579, говорит об отсутствии автокорреляции (рисунок 4.2.5. и приложение А)
2,026
![]()
![]()
![]()
![]() _______________________________________________
_______________________________________________
есть 0,69 ? 1,97 нет 2,03 ? 3,31 есть
(+) (-)
Рисунок 4.2.5. Таблица определения наличия или отсутствия автокорреляции на основе критерия Дарбина-Уотсона
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.