Экономика и менеджмент \ Статистика

Анализ временных рядов и прогнозирование в системе STATGRAFICS, страница 6

Forecast Table for RESIDUALS

Model: ARIMA(1,0,0)

                                     Lower 95,0%         Upper 95,0%        

Period           Forecast            Limit               Limit

------------------------------------------------------------------------------

2006             -0,033534           -0,477938           0,41087             

2007             -0,0122996          -0,485652           0,461053           

2008             -0,00451121         -0,481624           0,472602           

2009             -0,00165461         -0,479271           0,475962           

------------------------------------------------------------------------------

Рисунок 3.6.18.Прогноз остатков

Итоги прогнозирования обеспеченности жильем населения Хабаровского края сведены в таблице 3.6.1.

Таблица 3.5.1. Результаты прогнозирования обеспеченности жильем население Хабаровского края

Год прогноза

Прогноз по экспоненциальному тренду

Прогноз остатков

Граница прогноза остатков

Объединенный прогноз

нижняя

верхняя

2006

20,4697

-0,4779

-0,4779

0,41087

19,9918

2007

20,8701

-0,4857

-0,4857

0,4605

20,3844

2008

21,2783

-0,4816

-0,4816

0,4726

20,7967

2009

21,6945

-0,4793

-0,4793

0,4760

21,2152

Результаты прогнозирования свидетельствуют, что объединенный прогноз обеспеченности жильем меньше прогноза по экспоненциальному тренду  из-за отрицательного прогноза остатков. За прогнозируемые годы обеспеченность жильем вырастет на  6,1% и к 2009 году достигнет 21,21кв.м.

4.2. Прогнозирование на основе множественной корреляционно-регрессионной модели с помощью пакета STATGRAFICS

В системе STATGRAFICS реализовано несколько методов корреляционно-регрессионного анализа, позволяющих установить связь между результативным признаком и одним или более факторными переменными. В основном модуле Relate (Связи) представлены:

- Simple Regression (Простая регрессия);

- Polynomial Regression (Полиномиальная регрессия);

- Multiple Regression (Множественная регрессия) В этом модуле реализована возможность пошаговой регрессии.

С целью исключения мультиколлинеарных  факторов,  построим  множественную линейную модель, используя пошаговую регрессию.

Матрица исходной информации представлена в Приложении Б. В качестве исходной информации, используются следующие показатели:

У- Средняя обеспеченность населения жильём всего кв. м  общей площади  на одного жителя;

Х2 - Средняя стоимость строительства за 1 кв.м., руб (в сопоставимых ценах);

Х3 - Денежные доходы в расчете на душу населения в среднем за месяц,  тыс.руб. (в сопоставимых ценах);

Х4 - Удельный вес частного жилого фонда, %;

Х5 - Удельный вес числа семей, состоящих на учете  для получения жилья, в общем числе семей, %;

Х6 - Удельный вес семей улучшивших свои жилищные условия в % от числа семей, состоящих на учете на получение жилья;

Х7 -  Капитально отремонтированных жилых домов за год, всего тыс. кв. м, общей площади;

Х8 - Индекс потребительских цен (декабрь текущего года в % к декабрю предыдущего года);

Х9 -  Численность безработных, человек;

Х10 -  Ввод в действие жилых домов, тыс. кв. метров общей площади;

      Х11 - Инвестиции в  жилища млн. руб. (в сопоставимых ценах).

В главном меню выбираем модуль Relate (Связи) и находим процедуру Multiple Regression(Множественная регрессия). Система STATGRAFICS покажет входную панель множественной регрессии (рисунок 4.2.1.)

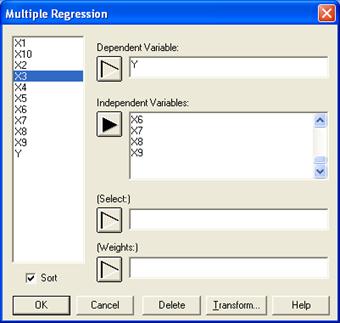
DependentVariable – Зависимая переменная; IndependentVariable– Независимые переменные; Select – Выбрать; Weights – Веса.

Рисунок 4.2.1. – Входная панель процедуры Multiple Regression(Множественная регрессия)

После нажатия клавиши OK появится окно с предварительными результатами анализа (рисунок 4.2.2.).

Multiple Regression Analysis

-----------------------------------------------------------------------------

Dependent variable: Y

---------------------------------------------------------------------------

                                       Standard          T

Parameter               Estimate         Error       Statistic        P-Value

-----------------------------------------------------------------------------

CONSTANT                 10,8613        2,00102        5,42791         0,0123

X1                     -0,137878       0,571198      -0,241384         0,8248

X10                     0,538811       0,358874        1,50139         0,2303

X2                       1,80787        2,10914       0,857156         0,4544

X3                      0,126905      0,0255044        4,97579         0,0156

X4                     0,0977076      0,0401923          2,431         0,0932

X5                     -0,168993       0,174397      -0,969015         0,4040

X6                  0,0000286517    0,000084697       0,338285         0,7574

X7                   -0,00139405      0,0010293       -1,35437         0,2686

X8                 -0,0000213316   0,0000217901      -0,978958         0,3998

X9                    0,00303274     0,00278768        1,08791         0,3562

-----------------------------------------------------------------------------

                           Analysis of Variance

-----------------------------------------------------------------------------

Source             Sum of Squares     Df  Mean Square    F-Ratio      P-Value

-----------------------------------------------------------------------------

Model                     27,4126     10      2,74126      80,89       0,0020

Residual                 0,101667      3    0,0338891

-----------------------------------------------------------------------------

Total (Corr.)             27,5143     13

R-squared = 99,6305 percent

R-squared (adjusted for d.f.) = 98,3988 percent

Скачать файл