Степенные ряды. Свойства степенных рядов в круге сходимости; понятие об аналитической функции. Ряд Тейлора. Разложение функции вещественной переменной в ряд Тейлора

Глава «Степенные ряды».................................................................................. 1

§1  Степенной Ряд; Круг И Радиус Сходимости............................................. 1

§2  Свойства степенных рядов в круге сходимости; понятие об аналитической функции................................................................................. 3

§3 Ряд Тейлора. Разложение функции вещественной переменной в ряд Тейлора......................................................................................................... 4

§4   Ряды Тейлора для функций e^x, sin(x), cos(x), ln(1+x).  Аналитические функции e^z, sin(z), cos(z);  формула Эйлера.................................................. 7

§5   Приложения рядов Тейлора для вычисления и интегрирования функций.       9

Глава «Степенные ряды»

§1  Степенной Ряд; Круг И Радиус Сходимости.

Пусть задана числовая последовательность .

Определение 1.  Степенным рядом называется ряд вида

Замечания.

1.  На комплексной плоскости  или на числовой прямой  степенной ряд определяет множество числовых рядов, одни из которых сходятся (абсолютно или условно), а другие – расходятся. Поэтому исследование степенного ряда сводится к установлению области его сходимости – множества

2.  (а) Всякий степенной ряд  сходится хотя бы в одной  точке ;  (б) существуют степенные ряды, сходящиеся только в одной точке;  (в)  существуют степенные ряды, сходящиеся на всей комплексной плоскости.

(а): z=z₀. èS_n(z₀)=a₀è

(б):    

( в)

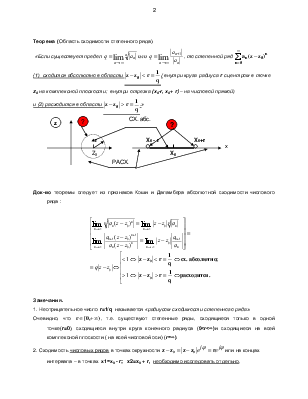
Теорема (Область сходимости степенного ряда).

 «Если существует предел , то степенной ряд

(1)  сходится абсолютно в области ( внутри круга радиуса r с центром в точке z₀ на комплексной плоскости;  внутри отрезка (х₀-r, х₀+ r) – на числовой прямой)

и (2) расходится в области .»

Док-во теоремы следует из признаков Коши и Даламбера абсолютной сходимости числового ряда :

Замечания.

1. Неотрицательное число r=1/q  называется «радиусом сходимости степенного ряда».

Очевидно, что , т.е. существуют степенные ряды, сходящиеся только в одной точке(r=0), сходящиеся внутри круга конечного радиуса (0<r<∞)и сходящиеся на всей комплексной плоскости ( на всей числовой оси) (r=∞).

2. Сходимость числовых рядов в точках окружности или на концах интервала – в точках  х1=x₀ - r;   x2=x₀ + r,  необходимо исследовать отдельно.

Пример. Исследовать область сходимости степенного ряда 

1.  По признаку Коши 

è 

2.  Сходимость на концах интервала :

Таким образом, степенной ряд 

(1)  сходится абсолютно  для  

(2)  сходится условно в точке x1= -1;

(3)  расходится 

§2  Свойства степенных рядов в круге сходимости; понятие об аналитической функции.

Пусть ст. ряд   сходится (абсолютно) в области D: |z|<r.

Тогда на множестве D задана комплексно-значная функция – сумма сходящего числового ряда

Определение.           Аналитической функцией называется функция (однозначное соответствие, отображение), задаваемая суммой степенного ряда в области его сходимости .

Например,  - аналитическая функция.

Свойства аналитической функции (свойства степенных рядов внутри круга сходимости).

1.  Степенной ряд внутри круга сходимости можно почленно дифференцировать и интегрировать, при этом радиус сходимости не изменяется.

2.  Аналитическая функция является непрерывно-дифференцируемой функцией (имеет непрерывные производные любого порядка), при этом производная и первообразная аналитической функции определяются суммой степенного ряда, полученного почленным дифференцированием и интегрированием исходного степенного ряда;  ó.

§3 Ряд Тейлора. Разложение функции вещественной переменной в ряд Тейлора.

Пусть функция    бесконечно дифференцируема в точке x₀, т.е. в некоторой окрестности точки существуют непрерывные производные любого порядка.

Из курса анализа известно, что  имеет место формула Тейлора порядка “n”