1. Исследовать систему на совместимость и решить методом Крамера.
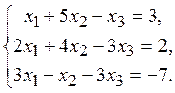
Решение:
Т-ма Крамера: крамеровская система имеет единственное решение.
Крамеровская система – это система, удовлетворяющая следующим 2-м условиям:
1) число уравнений системы = числу неизвестных
2) определитель, составленный из коэффициентов при неизвестных, отличен от 0
Составим определитель:
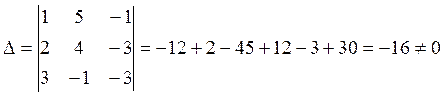
Система совместима, т.е. имеет хотя бы одно решение.
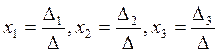
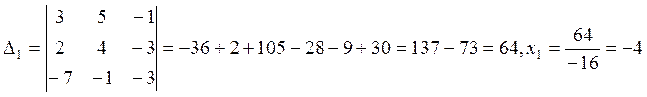
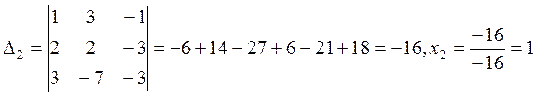
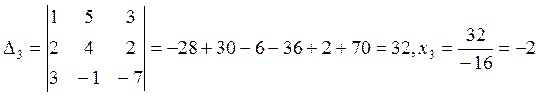
Ответ: (-4; 1; -2)
2. Решить систему линейных алгебраических уравнений методом Гаусса
![]()
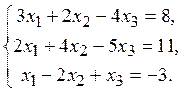 .
.
Решение:Выпишем
расширенную матрицу системы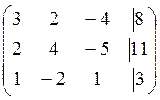
Приведем эту матрицу к ступенчатому виду. Для этого мы можем делать элементарные преобразования строк.
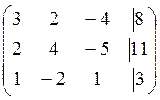
![]()
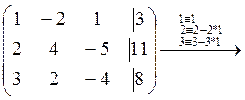
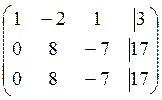
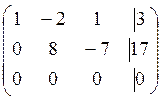
Т-ма
Кронекери-Копелли: СЛУ совместима ![]() , когда ранг матрицы =
рангу расширенной матрицы системы.
, когда ранг матрицы =
рангу расширенной матрицы системы.
Ранг матрицы – число ненулевых строк в ступенчатом виде матрицы
С – расширенная матрица системы, А – матрица системы
r(C)=2
r(A)=2 ![]() r(C)=r(A) и по теореме Кронекери-Копелли система совместима.
От ступенчатой матрицы переходим к ступенчатой системе:
r(C)=r(A) и по теореме Кронекери-Копелли система совместима.
От ступенчатой матрицы переходим к ступенчатой системе:
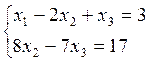
Т. к. число уравнений системы < числа неизвестных, то в этом случае система имеет бесконечно много решений. Чтобы найти решение, надо разбить неизвестные на главные и свободные.
![]() главные неизвестные,
главные неизвестные, ![]() свободная
неизвестная (может быть любым числом),
свободная
неизвестная (может быть любым числом),
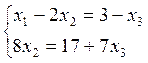
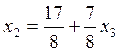
![]()
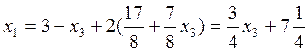
3. Разложить пространство R4 на прямую сумму подпространств размерности 2.
Решение:
R4 – множество строк длины 4 (4-х мерное арифметическое пространство)
R4={(![]()
Если А и В – подпространства пространства V, то через А+В обозначают множество {a+b|aЄA, bЄB}
В
случае, если А∩В={Ø} – нулевое подпространство, то такая сумма V=A+B
называется прямой и в этом случае пишут V=A![]() . В нашем случае Ø=(0,0,0,0)
. В нашем случае Ø=(0,0,0,0)
Пусть
теперь А={(![]() B={(0,0,
B={(0,0,![]()
Проверим, что пространство задаётся в виде А+В
Пусть![]()
![]()
а=(![]() в==(0,0,
в==(0,0,![]() ,
значит R4 =A
,
значит R4 =A![]() .
.
Ответ:
R4 =A![]() , где А={(
, где А={(![]() B={(0,0,
B={(0,0,![]()
4. Докажите, что в пространстве M(2, R)
система векторов 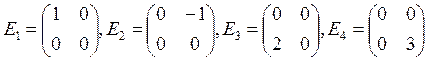 линейно независима.
линейно независима.
Решение:
Система векторов а1,а2,а3,а4 линейно независима, если в любой системе вида
![]() Ø
Ø ![]()
В
нашем случае, пусть 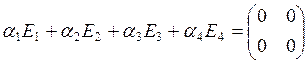
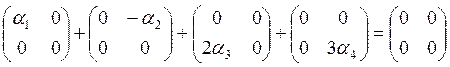
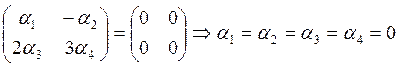
Значит, система векторов Е1, Е2, Е3, Е4 линейно независима.
5. Найдите
жорданову нормальную форму матриц: 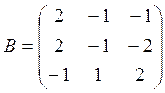 .
.
Решение:
Жорданова нормальная форма матрицы состоит из клеток Жордана вдоль главной диагонали, а все остальные элементы такой матрицы нулевые.
Клетка
Жордана – это матрица вида: 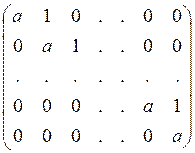
Если размер клетки n*n, то она обозначается символом Yn(a).
Пример: Y1(a)=а, Y2(a)=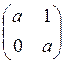 , Y3(a)=
, Y3(a)=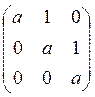
В искомой матрице записывают характеристический многочлен матрицы А и находят его корни.
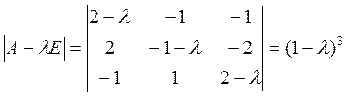
Характеристический
многочлен имеет единственный корень ![]() кратности 3.
кратности 3.
Надо выяснить, какой из 3-х случае нам подходит:
Y1=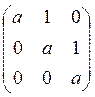 , Y2=
, Y2=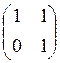 , Y3=(1)
, Y3=(1)![]()
Число всех клеток Жордана вычисляют по формуле:
![]()
A-E =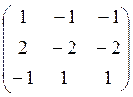 ~
~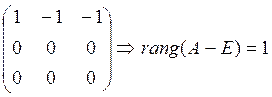
Значит,
![]() . Искомая матрица имеет вид: Y=
. Искомая матрица имеет вид: Y=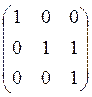
Ответ:
Y=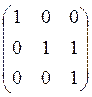
6. Исследовать, являются ли векторы
![]()
векторного пространства ![]() линейно зависимыми.
линейно зависимыми.
Решение:
Пусть 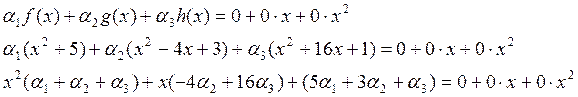
Это приводит к системе:
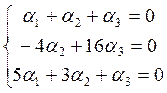
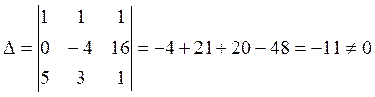
Т. к. определитель системы ≠ 0, то система имеет единственное нулевое решение. Значит, система векторов f(x), g(x), h(x) являются линейно независимыми.
Ответ: линейно независимы.
7. Найти собственные значения и собственные векторы линейного оператора пространства R2, заданного в некотором базисе матрицей
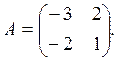 .
.
Решение:
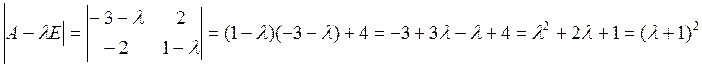
Характеристический многочлен
имеет единственный корень ![]() кратности 2.
кратности 2.
Значит, ![]() - собственное значение линейного
оператора.
- собственное значение линейного
оператора.
Найдем собственный вектор, отвечающий найденному собственному значению:
Пусть х = (х1, х2)
![]() х(А-
х(А-![]()
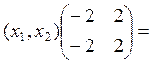 θ
θ
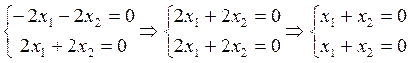
Пусть х2=t →x1=-t, где t – любое число
Ответ: собственное значение λ = -1, собственный вектор (-t, t), t – любое число.
8. Найти все значения ![]() , при
которых вектор
, при
которых вектор ![]() линейно выражается
через векторы
линейно выражается
через векторы
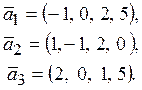
Решение:
Мы должны найти все λ, для
которых уравнение ![]() (1)
(1)
имеет решение 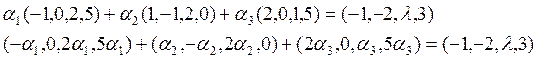
что приводит к системе: 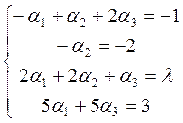
Уравнение (1) имеет решение ↔, когда данная система имеет решение. А согласно теореме Кронекери-Копелли данная система совместима ↔ ранг матрицы системы совпадает с рангом расширенной матрицы.
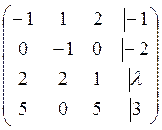 ~
~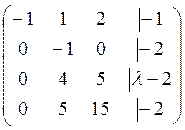 ~
~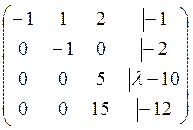 ~
~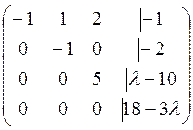
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.