При 18-3λ=0, т.е. при λ=6, ранг матрицы системы совпадает с рангом расширенной матрицы системы и = 3. И при таких λ система, а, значит, уравнение (1), имеет решение. При других λ решений нет.
Ответ: λ = 6
9. Найти базис и размерность линейной оболочки 
векторов из 
, где 
Решение:
Рассмотрим систему векторов 
, 
. И
пусть 
θ, θ=0+0х+0х2
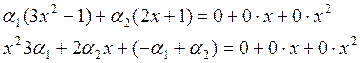
Это приводит к системе:
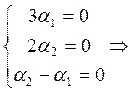Система
имеет единственное решение:
И поэтому вектора, линейно
независимы.
Рассмотрим систему векторов , , 
(1)
Пусть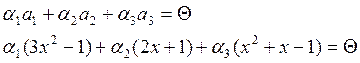 
Это приводит к системе: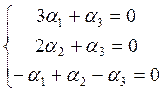 
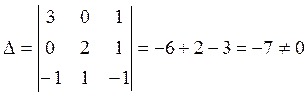
Определитель системы ≠ 0 → система имеет единственное нулевое решение. Значит, система векторов (1) является базисом линейной оболочки. LimL(a1, a2, a3)=3
Ответ: базис: , , , LimL(a1, a2, a3)=3
10.
Докажите, что линейные
пространства 
и 
изоморфны:
C над R ,
R2.
Решение:
Т-ма: 2 конечномерных векторных пространства изоморфны ↔, когда их размерности совпадают.
Размерностью пространства V (dim V) называется число элементов в базисе этого пространства. Найдем базисы для V1 и V2.
Для любого комплексного числа zЄV1 мы имеем: z = a+bi=0.1+0, любое комплексное число – есть линейная комбинация векторов 1, i (1).
Пусть
теперь 
, значит система (1) линейно независима и
поэтому является базисом в пространстве V1. Итак, dimV1=2
В пространстве R2 имеется базис e1=(1,0), e2=(0,1). Значит dimV2=2.
Следовательно, по теореме эти пространства изоморфны.
11 Найти матрицу, обратную матрице А
.
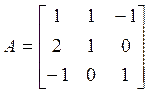Решение: Обратную матрицу можно искать только для квадратной матрицы, у которой определитель ≠ 0
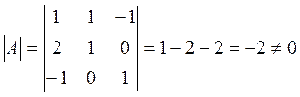т. к. 
обратная матрица
существует
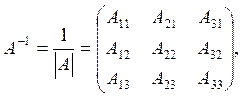Aij - алгебраические дополнения
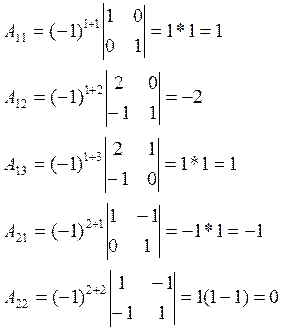
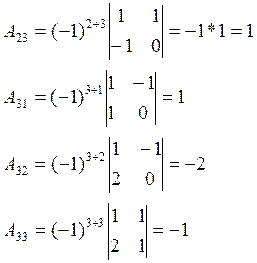
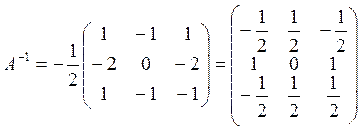Ответ: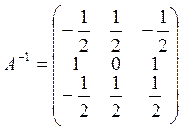 
12. Докажите, что множество решений однородной системы линейных уравнений образует линейное пространство над R:
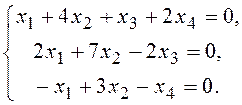
Решение:
Найдем решение данной системы линейных уравнений:
~
~
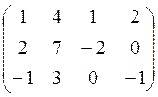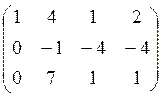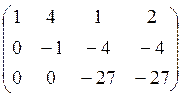
Преобразованная система имеет
вид: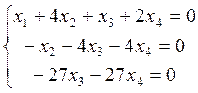
Т.к число уравнений системы < числа неизвестных, то в этом случае система имеет бесконечно много решений. Чтобы найти решение, надо разбить неизвестные на главные и свободные: х1, х2, х3 – главные неизвестные, х4 – свободная неизвестная.
х1=-4*0+х4-2х4=-х4, х4 – любое действительное число, х4=α.
Тогда множество всех решений данной системы можно записать как множество:
V={(-α, 0, -α, α)| αЄR}. Пусть у, х ЄV, тогда х+у = (-α1-α2, 0, -α1-α2, α1+α2)=(-( α1+α2), 0, -( α1+α2), α1+α2). Пусть α1+α2=α, α ЄR. Значит, х+уЄV , βх =(-βα1, 0, -βα1, βα). Пусть βα1=α, αЄR. Значит βх ЄV.
1) Пусть z =(-α3, 0, - α3, α3)
(x+y)+z=(-(α1+α2+α3), 0, -(α1+α2+α3), α1+α2+α3)=(-α1-(α2+α3), 0, -α1-(α2+α3), α1+(α2+α3))=x+y+z
2) θ=(0, 0, 0, 0) – нулевой элемент
3) для любого х == (-α, 0, -α, α) ЄV существует противоположный элемент (-х)= (-α, 0, -α, α) ЄV
4) х+у = (-α1, 0, -α1, α1)+ (-α2, 0, -α2, α2)= (-(α1+α2), 0, -(α1+α2), α1+α2)= (-(α2+α1), 0, -(α2+α1), α2+α1)=у+х для любого х,у ЄV
5) (γβ)x=γ(βx) для любого х ЄV, γ,βЄR
6) 1*x=x для любого х ЄV
7) β(х+у)=βх+βу для любого βЄR, x,y ЄV
8) (γ+β)x=γx+βy для любого β, γЄR, x ЄV
Следовательно, множество V является линейным пространством над R.
13. Даны два базиса 
и 
пространства
Найти матрицу перехода от базиса 
к 
.
Решение:
Так как векторы е1, е2 образуют базис пространства, то векторы а1 и а2 можно линейно выразить через е1, е2:
а1=α11е1+α12е2 или (-2, -4)=α11(1, -2)+ α12(3, 2)
а2=α21е1+α22е2 (-1, -6)= α21(1, -2)+ α22(3, 2)
Каждое
из этих равенств можно заменить системой уравнений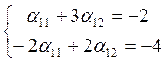 
α11=1,
α12= -1.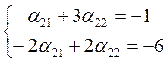 
α21=2, α22=
-1
Тогда
матрица перехода: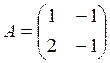 
Ответ:
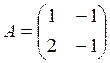
14. Найти ранг матрицы А
.
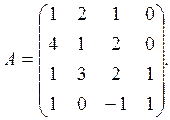Решение:
Приведем данную матрицу к ступенчатому виду:
~
~
~
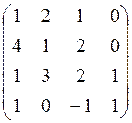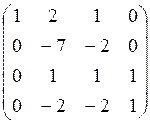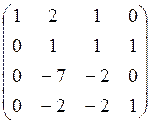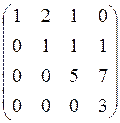
r(A)=4 (число ненулевых строк в ступенчатом виде матрицы)
Ответ: r(A)=4
26. Исследовать на дифференцируемость функцию
Решение: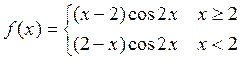 
Подозрение вызывает точка x=2.
Воспользуемся теоремой: для того, чтобы 
была
дифференцируемой в точке 
чтобы
она имела производную в этой точке. Найдём левостороннюю и правостороннюю
производные.
1)
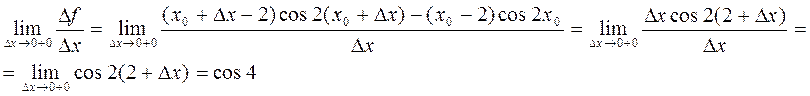
2) 
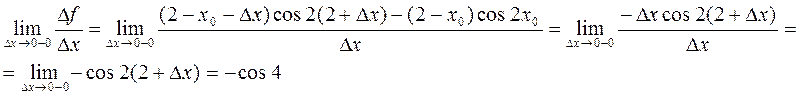
Т.е. левосторонний предел ¹правостороннему, значит производной в точке х=2 не $ Þ по теореме функция f(x) не дифференцируема в точке x0=2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.