16.Понятие производной по направлению от функции 2х и 3х переменных, ее механический смысл и связь с частными производными.
Рассмотрим случай функции двух переменных.
Пусть
в области D, плоскости Оху задана ф–ция z=f(M)=f(x,y).
Пусть задан ненулевой вектор ![]() , с направляющими
косинусами
, с направляющими
косинусами ![]() .Исходя из точки М(х,у) области D
перейдём в точку M1(x+Δx,y+Δy)
этой области, двигаясь в направлении вектора
.Исходя из точки М(х,у) области D
перейдём в точку M1(x+Δx,y+Δy)
этой области, двигаясь в направлении вектора ![]() .
.
Пусть
![]() (1)
(1)
Пусть Δz - полное приращение функции z в точке М. Δz=f(M1)–f(M).
Опр: Предел ![]() , если он существует и
конечен , называется производной от функции z=f(M)=f(x,y) по
направлению
, если он существует и
конечен , называется производной от функции z=f(M)=f(x,y) по
направлению ![]() и обозначается
и обозначается ![]()
Ясно, что частные производные являются частным случаем производной по направлению.
Теорема: Пусть функция z=f(x,y)
дифференцируема в точке М(х,у), тогда производная от функции z в
точке М по направлению ![]() существует, каков бы не был
вектор
существует, каков бы не был
вектор ![]() , причём
, причём
![]() (2), где
(2), где
![]() - направляющие косинусы вектора
- направляющие косинусы вектора ![]() .
.
Доказательство: т.к. функция z дифференцируема в точке М, то Δz=Δf(M) может быть представлен в виде
![]() (3), где
ε1→0, ε2→0 при Δx→0,
Δy→0, а значит и при Δl→0.
(3), где
ε1→0, ε2→0 при Δx→0,
Δy→0, а значит и при Δl→0.
Поделим (3) почленно на Δl и воспользуемся равенством (1). Получим:
![]()
Переходя к пределу при Δl→0 получим равенство (2):
![]() .
.
17. Понятие градиента ф–ций двух и трех переменных. Св–ва.
Опр: Вектор ![]() называется градиентом
функции z=f(M) и обозначается символом grad f(M), или
grad f(x,y), или grad z.
называется градиентом
функции z=f(M) и обозначается символом grad f(M), или
grad f(x,y), или grad z.
![]() (4)
(4)
Используя понятие градиента функции f(M) преобразуем (2).
Пусть
![]() - единичный вектор в направлении
- единичный вектор в направлении ![]() .
. ![]() в силу
(2) и (4) будет
в силу
(2) и (4) будет
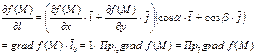
Т.о. (2) можно записать в виде
![]() (5).
(5).
Равенство (5) показывает, что grad f(M) задает направление наибыстрейшего возрастания функции f(M) в точке М.
Все сказанное переносится на случай более чем двух переменных.
Теорема 2: Пусть M0(x0,y0) - обыкновенная точка некоторой линии уровня поверхности z=f(x,y). Тогда вектор grad f(M) направлен по нормали к линии уровня поверхности z=f(x,y), проходящей через точку M0.
Следствие: Если вектор ![]() направлен
по касательной к линии уровня поверхности z=f(x,y),
проходящей через точку M0, то
направлен
по касательной к линии уровня поверхности z=f(x,y),
проходящей через точку M0, то ![]() .
.
Д–во: Пусть C=f(x0,y0), тогда линия уровня, проходящая через M0, задаётся уравнением f(x,y)=C; F(x,y)–C=0. Уравнение касательной к этой линии в точке M0 имеет вид

А
это значит, что вектор ![]() , т. е. grad f(M0) направлен
по нормали к касательной, а следовательно по нормали и к линии уровня.
, т. е. grad f(M0) направлен
по нормали к касательной, а следовательно по нормали и к линии уровня.
Замечание: grad f(M0) всегда направлен в сторону выпуклости линии уровня точки M0.
18. Понятие квадрируемой плоскости области и ее площади. Интегральные суммы для функции двух переменных по квадрируемой области, их геометрический смысл. Определение двойного интеграла.
Опр: Пусть Q ограниченная плоская фигура. Если значение S точной верхней грани множества площадей всех многоугольников, вписанных в Q совпадает со значением точной нижней грани множества площадей многоугольников описанных вокруг Q, то фигура Q называется квадрируемой, а число S называется площадью этой фигуры.
Опр: Диаметром ограниченной плоской фигуры Q
называется величина ![]() .
.
Пусть на плоскости Оху задана область D (замкнутая или открытая безразлично) квадрируемая. Пусть в D определена ограниченная ф–ция z=f(x,y)=f(M). Разобьем область D на n квадрируемых частей D1,D2,…,Dn никакие две из которых не имеют общих точек.
Пусть
dk - диаметр части Dk, а ΔSk - площадь этой части (k=1,2,…,n). Пусть ![]() , λ -
ранг произвольного разбиения области D на частичные области.
, λ -
ранг произвольного разбиения области D на частичные области.
На каждой части Dk возьмем произвольную точку Mk(xk,yk), k=1,2,…,n и составим сумму
![]() (1)
(1)
Суммы вида (1) называются интегральными суммами, а точки Mk - промежуточными точками.
Опр: Число I называют конечным пределом интегральных сумм (1) при λ→0, и
пишут ![]() , если для любого ε>0 найдётся δ>0
такое, что для любого разбиения области D на частичные
области Dk, не имеющие общих внутренних точек, с условием λ<δ и
любого способа выбора промежуточных точек Mk в
частичных областях Dk выполняется равенство |σ–I|<ε.
, если для любого ε>0 найдётся δ>0
такое, что для любого разбиения области D на частичные
области Dk, не имеющие общих внутренних точек, с условием λ<δ и
любого способа выбора промежуточных точек Mk в
частичных областях Dk выполняется равенство |σ–I|<ε.
Опр: Если существует конечный предел интегральных сумм при λ→0, то он называется двойным интегралом от функции f(x,y) по области D и обозначается символами
![]() или
или ![]() , где dS=dxdy
называется элементом площади области D или элементарной площадью в
области D.
, где dS=dxdy
называется элементом площади области D или элементарной площадью в
области D.
Если
двойной интеграл ![]() существует, то функция f(x,y)
называется интегрируемой в области D.
существует, то функция f(x,y)
называется интегрируемой в области D.
Выясним геометрический смысл двойного интеграла в случае, если f(x,y) непрерывна и положительна в области D.
Очевидно слагаемое f(xk,yk)ΔSk интегральной суммы (1) дает объем цилиндра с основанием Dk и высотой f(xk,yk). Вся интегральная сумма (1) даст приближенно объем цилиндра Т. Причем погрешность приближается к 0 при λ→0. Следовательно двойной интеграл дает объем цилиндра Т.
19.Основные свойства двойного интеграла.
1.![]() 2.
2. ![]()
3. Если f(x,y) непрерывна в замкнутой области D, то она в этой области интегрируема.
4. Если
f(x,y) интегрируема в D1 и D2, не
имеющих общих внутренних точек и D1ÈD2 - область,
то функция f(x,y) интегрируема в области D1ÈD2, причём
![]() 5. Свойство линейности: Если функции f(x,y) и g(x,y)
интегрируемы в области D, то в D интегрируема и функция α.f(x,y)+β.g(x,y), причем
5. Свойство линейности: Если функции f(x,y) и g(x,y)
интегрируемы в области D, то в D интегрируема и функция α.f(x,y)+β.g(x,y), причем
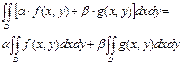
6. Если функции f(x,y) и g(x,y) интегрируемы в области D, то и произведение f(M).g(M) также интегрируемо в этой области.
7. Если
функции f(x,y) и g(x,y) интегрируемы в области D и всюду в D f(M)£g(M), то ![]() .
.
8. Если
функция f(x,y) интегрируема в области D и всюду в D С1£f(M)£C2, то ![]() .
.
Формула
среднего значения: Если функция f(x,y) непрерывна в замкнутой области D, то
найдётся точка M0ЄD
такая, что ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.