Федеральное агентство по образованию
Санкт-Петербургский государственный горный институт им. Г.В.Плеханова
(технический университет)
Кафедра механики
РГР №1
Расчет статически неопределимых стержневых систем
Вариант 1
Выполнила: студента группы ТО-07
Артов П.А.
Проверил:
Санкт-Петербург
2009г
Формулировка задания
Рассчитать площадь поперечного сечения стержней указанной конструкции:
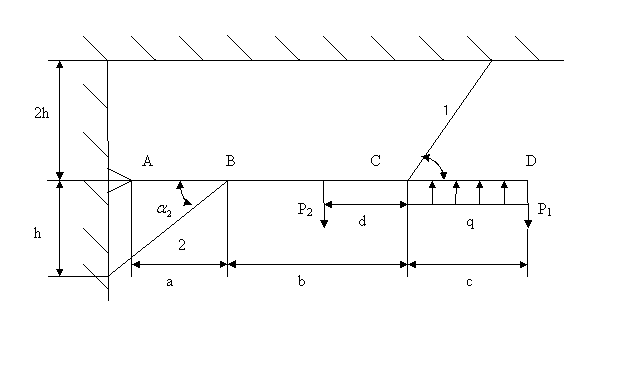
Рассчитываемая система представляет собой стержневую конструкцию с
одной шарнирной опорой и двумя деформируемыми тягами. Заданы материалы стержней
1 – медь, 2 – сталь, модули упругости их при растяжении – сжатии: Е1=
![]() МПа; Е2=
МПа; Е2=![]() МПа. Внешняя сила Р1,
действующая на конструкцию, равна – 20кН, а внешняя сила Р2,
действующая на конструкцию, равна – 10кН, q = 20кН/м.
Стержень один изготовлен на 0,001м длиннее. Стержень два нагревается на 20
градусов Цельсия. Конструкционные соотношения площадей стержней F2/F1 =1.
Геометрические размеры системы: а=2м; b=5м; с=4м; d=2м; h=2м;
МПа. Внешняя сила Р1,
действующая на конструкцию, равна – 20кН, а внешняя сила Р2,
действующая на конструкцию, равна – 10кН, q = 20кН/м.
Стержень один изготовлен на 0,001м длиннее. Стержень два нагревается на 20
градусов Цельсия. Конструкционные соотношения площадей стержней F2/F1 =1.
Геометрические размеры системы: а=2м; b=5м; с=4м; d=2м; h=2м; ![]() ;
;
![]() . Предполагается что балка абсолютно
жесткая и невесомая.
. Предполагается что балка абсолютно
жесткая и невесомая.
Расчет усилий от внешних сил Р1, Р2 и Q
Для расчетов усилий используем метод сечений. Сечения проведем через оба стержня. Составим уравнение статики:
![]() , (1)
, (1)
где Q=qc.
Остальные уравнения статики можно не составлять, так как они необходимы только при определении реакций в шарнире ХА, YА, чего не требуется по условию задачи.
Таким образом степень статической неопределенности К=1, так как система имеет два неизвестных усилия R1, R2 и одно уравнение статики.
Для составления условий совместности деформаций необходимо рассмотреть схему перемещений элементов системы:
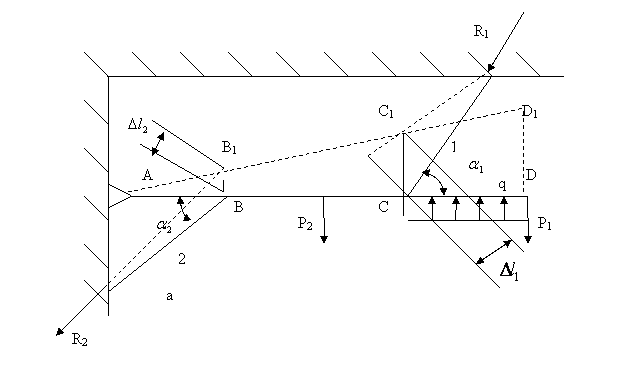
Под действием внешних сил Р1, Р2 и Q первый стержень укоротиться на
величину ![]() , а второй стержень удлиниться на
величину
, а второй стержень удлиниться на
величину![]() , при этом жесткая балка AD, повернется в положение АD1.
Ввиду малости деформации точек В и С в ходе деформации перемещаются вертикально
и займут положение В1 и С1. Положение этих точек
определяется пересечением линии АD1 и
перпендикуляров, проведенных к первоначальному направлению осевой линии балки AD в точки В и С. Удлинение
, при этом жесткая балка AD, повернется в положение АD1.
Ввиду малости деформации точек В и С в ходе деформации перемещаются вертикально
и займут положение В1 и С1. Положение этих точек
определяется пересечением линии АD1 и
перпендикуляров, проведенных к первоначальному направлению осевой линии балки AD в точки В и С. Удлинение ![]() и
и
![]() находим также графически, для чего
из точек С и В опустим перпендикуляры на линии соответствующих новым положениям
стержней 1 и 2 после приложения нагрузки Р1, Р2 и Q. Отрезки В1В2 и С1С2
определяют удлинение стержней соответственно
находим также графически, для чего
из точек С и В опустим перпендикуляры на линии соответствующих новым положениям
стержней 1 и 2 после приложения нагрузки Р1, Р2 и Q. Отрезки В1В2 и С1С2
определяют удлинение стержней соответственно ![]() и
и
![]() .
.
Условие совместной деформации в данном случае проще всего составит, воспользовавшись подобием треугольников АВ1В и АС1С:
![]() ; (2)
; (2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.