Расчет статически неопределимой стержневой системы. Вариант № 1, страница 2

Также определим:

; .                                                              (3)

Подставим выведенные значения ВВ₁ СС₁ в тождество, полученное исходя из свойств подобия треугольников АВ₁В и АС₁С, получим условие совместной деформации для заданной стержневой системы:

;                                                                                                   (4)

или

;

где ==6,09 - безразмерный коэффициент, учитывающий особенности геометрической конфигурации системы.

Используя закон Гука для каждого из стержней, из условия совместной деформации, для заданной системы, получим:

, по условию =1F₁=F₂, Е₁=1МПа; Е₂=МПа.

Учитывая, что =4,6(м), а =4(м) - длины стержней, последнее соотношение можно переписать следующим образом:

.                                                                                       (5)

Далее решаем совместно систему уравнений (5) и (1):

;

.

;

.

;

.

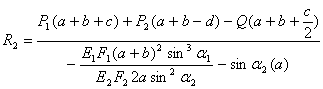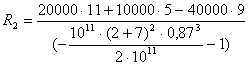R₂=5353,9H5,35МН(растяжение);

R₁13,9МН(сжатие).

Произведем проверку правильности найденных значений, для этого необходимо подставить полученные значения в уравнение равновесия (1):

0

Так как значения выражения, при подстановке вычисленных значений R₁ и R₂, приблизительно равно нулю то значит R₁ и R₂ вычислены верно.

Определение напряжений, вызванных неточностью изготовления

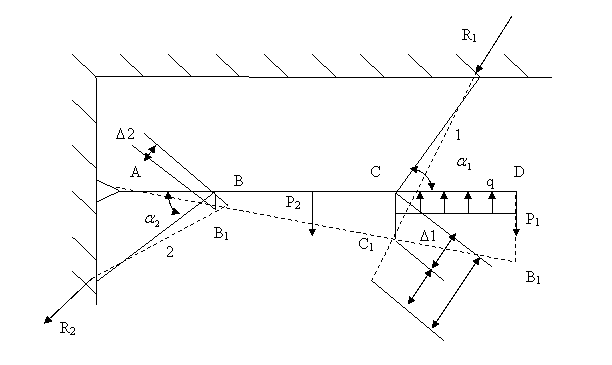
Так как первый стержень изготовлен с неточностью по длине ,  то при сборке конструкции в стержнях появятся внутренние напряжения. Расчетная схема будет выглядеть так:

                                                                                                               

1 стержень - сжатие; 2 стержень - сжатие.

Из схемы перемещений получим:

В₁В₂==; С₁С₂==.