Прохождение детерминированных сигналов через линейные цепи

Опыт – отец всякой достоверности.

Мудрость – дочь опыта.

Леонардо да Винчи

 Глава 6

ПРОХОЖДЕНИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ

6.1.         Изучаемые вопросы

Спектральный, операторный и временной методы анализа передачи сигналов через линейные цепи. Передача управляющих сигналов через апериодические цепи, включая активные фильтры. Дифференцирование и интегрирование сигналов [1, 6.1…6.5; 3, 5.1…5.5; 2, 8.1…8.3].

Прохождение модулированных колебаний через узкополосные избирательные цепи, точные и приближённые методы. Прохождение радиоимпульсов, ЧМ-колебаний, фазо- и частотно-модулированных колебаний [1, 6.6…6.11; 3, гл.7; 2, 9.3].

Указания. При изучении вопросов необходимо чётко уяснить целесообразность использования того или иного метода исследования. В случае анализа радиосигналов в избирательных цепях следует ясно представить возможности и ограничения приближённых методов (спектрального, комплексной огибающей, интеграла наложения и мгновенной частоты).

Простейшие линейные цепи с использованием операционных усилителей (ОУ) и активные фильтры рекомендуем изучать по книгам [3, 17].

Руководства [5…7] содержат большое число задач с комментариями и решениями.

В настоящей главе рассматриваются три класса задач: первый – прохождение видеосигналов через апериодические цепи (включая интегрирующие и дифференцирующие), второй – воздействие импульсных сигналов на избирательной цепи, третий – прохождение радиосигналов через резонансные цепи.

6.2.         Краткие теоретические сведения

При исследовании прохождения сигналов через линейные цепи можно использовать прежде всего известные из курса “Основы теории цепей” методы такие, как классический метод дифференциальных уравнений, метод интеграла наложения (Дюамеля) и спектральный (операторный).

Выбор соответствующего метода зависит от вида (сложности) входного сигнала, структуры цепи и от того, в какой форме (временной или частотной) требуется представить выходной сигнал.

При воздействии простейших сигналов на цепи, описываемые дифференциальными уравнениями не выше второго порядка, исследования можно проводить классическим методом. Для сложных сигналов и сложной структуры цепей следует применять либо метод интеграла наложения, либо спектральный (операторный) метод. Отметим, что спектральный и временной подходы полностью эквивалентны друг другу и базируются на принципе суперпозиции.

В основе метода интеграла наложения лежит импульсная характеристика цепи :

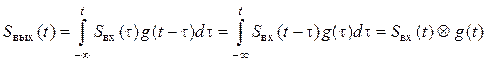, (6.1)

т. е. сигнал на выходе линейной цепи является сверткой входного сигнала и импульсной характеристики.

В основе спектрального метода исследования линейных цепей лежит использование спектральной плотности  входного сигнала  и передаточной функции цепи . При этом выходной сигнал в частотной и временной областях

,                               (6.2)

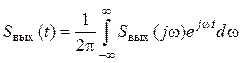.                           (6.3)

Связь между сигналами и их спектрами, а также между импульсной и частотной характеристиками цепи определяется парой преобразований Фурье (2.8), (2.9) и (5.4). Преимуществом данного метода является наглядность представления в виде спектров (совокупности гармонических колебаний) и деформации спектров в соответствии с частотными характеристиками цепи.

При операторном методе вместо преобразований Фурье используют преобразования Лапласа. Тогда напряжение на выходе цепи

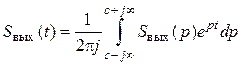,                           (6.4)

где

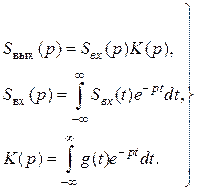                                (6.5)

Этот метод уступает предыдущему в наглядности, но при его использовании большая часть формальных вычислений может быть сокращена за счёт применения широко распространённых таблиц преобразований Лапласа (например, прил. П.6).

В табл. 6.1. приведены коэффициенты передачи некоторых активных RC-фильтров [17].

Для сложных функций  можно перейти от интеграла вида (6.4) к сумме вычетов, т. е.

,                                       (6.6)

где  – сумма вычетов в полюсах подынтегральной функции (6.4).

Если функция  дробно-рациональная, причём степень полинома  меньше степени полинома , то вычет этой функции, имеющей в точке  простой полюс (первой кратности), определяется по формуле

.

Таблица 6.1

Если функция  имеет в точке  полюс кратности  (при этом  – целое положительное число), то

.

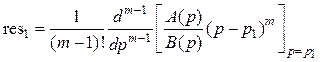Применение теории вычетов может упростить расчёт цепи операторным методом.

При определении требуемой характеристики сигнала или цепи необходимый метод расчёта (алгоритм) с минимальным количеством интегральных операций может быть выбран с помощью схемы (графа) (рис. 6.1.).

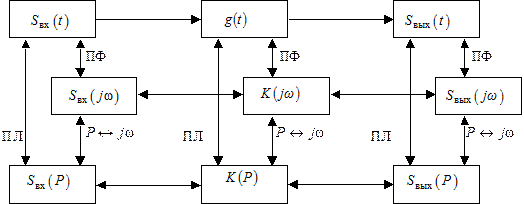
Рис. 6.1

При исследовании прохождения модулированных (узкополосных) сигналов через узкополосные (избирательные) цепи, полоса пропускания которых мала по сравнению с центральной частотой, кроме перечисленных методов, дающих точное решение, используются также и приближённые методы (рис. 6.2), которые в ряде случаев дают решения, весьма близкие к точным.

Суть метода комплексной огибающей состоит в следующем. Узкополосное колебание  представляется в комплексном виде согласно (3.7)…(3.9), т. е.

,                         (6.7)

где – комплексная огибающая, содержащая всю информацию, заложенную в сигнал  в результате амплитудной и угловой модуляции. Предполагаем, что центральная (резонансная) частота  цепи отличается расстройкой  от несущей частоты  входного сигнала, т. е. . Тогда