Другие предметы \ Радиотехнические цепи и сигналы

Прохождение детерминированных сигналов через линейные цепи, страница 5

6.4.2. Прохождение импульсных сигналов через избирательные цепи

Постоянная ЭДС В подключается к входу контура (рис. 6.16 и 6.17). Схема контура, его параметры и подлежащая определению реакция контура приведены в табл. 6.3.

Требуется определить соответствующую реакцию на заданное входное воздействие.

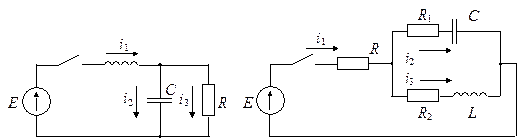
Рис. 6.16 Рис. 6.17

Таблица 6.3

Номер варианта	Контур	Реакция	Номер подварианта	, Ом	, Ф	, Гн
0	Рис. 6.16		0	100	10^–5	10^–3
1	"		1	80	5×10^–6	5×10^–3
2	"		2	40	10^–6	10^–4
3	"		3	20	5×10^–5	5×10^–4
4	"		4	10	10^–5	10^–2
5	Рис. 6.17		5	100	10^–4	10^–3
6	"		6	150	5×10^–5	5×10^–3
7	"		7	200	10^–5	10^–1
8	"		8	250	5×10^–6	0,5×10^–2
9	"		9	300	10^–6	10^–2

6.4.3. Прохождение радиосигналов через избирательные цепи

На колебательный контур (рис. 6.18) воздействует модулированное колебание, параметры которого указаны в табл. 6.4 и 6.5. Контур имеет следующие параметры: , кОм, , Ом.

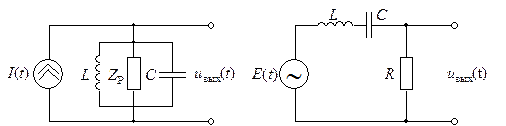
а б

Рис. 6.18

Таблица 6.4

Номер варианта	Схема	Вид модуляции	Входной сигнал
0	Рис. 6.18, а	ЧМ
1	Рис. 6.18, б	ЧМ
2	Рис. 6.18, а	ФМ
3	Рис. 6.18, б	ФМ
4	Рис. 6.18, а	АМ
5	Рис. 6.18, б	АМ
6	Рис. 6.18, а	АМ
7	Рис. 6.18, б	АМ
8	Рис. 6.18, а	Режим несущей
9	Рис. 6.18, б	Режим несущей

Таблица 6.5

Номер подварианта	, мА	, B	, MГц	, кГц	Вариант		Модулирующая функция
					0–3	4–7
					, рад
0	0.10	1.0	1.0	1.0	10.0	0.50
1	0.9	9.0	1.0	2.0	5.0	0.25
2	0.8	8.0	0.75	3.0	2.5	0.75
3	0.7	7.0	0.8	4.0	2.0	0.50
4	0.6	6.0	0.5	5.0	1.0	0.75
5	0.5	5.0	1.2	6.0	2.0	0.50
6	0.4	4.0	0.7	7.0	1.0	0.25
7	0.3	3.0	1.6	8.0	2.0	0.50
8	0.2	2.0	0.9	9.0	1.0	0.75
9	2.0	1.0	2.0	10.0	2.0	0.25

Требуется:

а) получить выражение для напряжения на контуре;

б) построить временную диаграмму огибающей напряжения на контуре и временную диаграмму огибающей входного сигнала;

в) для АМ колебания определить величину демодуляции, рассчитать спектр колебания на контуре и построить спектральные диаграммы амплитуд и фаз.

Методические указания

При выполнении вариантов 0–3 целесообразно воспользоваться методом “мгновенной” частоты, а при выполнении вариантов 4–9 – спектральным методом или методом комплексной огибающей.

1 2 3 4 5

Скачать файл