Прохождение детерминированных сигналов через линейные цепи, страница 2

,                         (6.8)

,                         (6.9)

где слагаемое  в (6.8) отнесено к фазовому сдвигу сигнала . На выходе заданной цепи получится также комплексный сигнал

,                  (6.10)

действительная часть которого

               (6.11)

и представляет собой выходной сигнал.

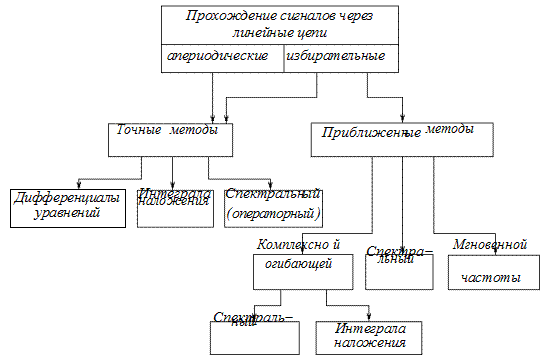Рис. 6.2

Итак, задача сводится к тому, чтобы определить влияние цепи на комплексную огибающую входного сигнала. В зависимости от того, частотные или временные характеристики цепи заданы, задачу можно решить спектральным методом или методом интеграла наложения.

В первом случае спектральная плотность комплексной огибающей  выходного сигнала определяется произведением

=,                               (6.12)

где  – передаточная функция низкочастотного эквивалента цепи, получаемая смещением правых ветвей АЧХ  и ФЧХ  узкополосной цепи на частоту влево, в область низких частот.

Схемы низкочастотных эквивалентов некоторых избирательных цепей и их характеристики даны в [3, табл.7.1].

Комплексная огибающая выходного сигнала

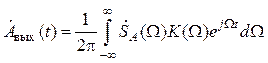                       (6.13)

и сам выходной сигнал

.                             (6.14)

Во втором случае, когда известна импульсная характеристика низкочастотного эквивалента , комплексная огибающая выходного сигнала

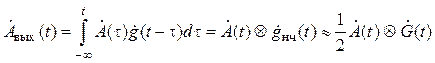,      (6.15)

т. е. является сверткой комплексной огибающей входного сигнала и комплексной огибающей импульсной характеристики низкочастотного эквивалента цепи (или с половиной комплексной огибающей импульсной характеристики цепи).

Приближённый спектральный метод используется при решении задач прохождения широкополосного сигнала через узкополосную цепь. При этом считается, что спектральные характеристики  и  входного сигнала приблизительно постоянны в пределах полосы пропускания цепи, т. е.

.                       (6.16)

Спектральное и временное представление выходного сигнала:

,

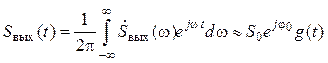.                (6.17)

где – импульсная характеристика линейной избирательной цепи, определяемая обратным преобразованием Фурье от передаточной функции .

Приближённый метод мгновенной частоты (иначе метод медленно меняющейся частоты) применяют при исследовании прохождения колебаний модуляции (или манипуляции) через резонансные цепи. При этом полагаем, что мгновенная частота входного сигнала изменяется достаточно медленно, так что установление стационарных колебаний на выходе происходит почти одновременно с изменением частоты на входе цепи. Используя символический метод, получаем:

;

;

;

,

где  – закон изменения видеосигнала (модулирующего сигнала). Для мгновенной частоты имеем

.       (6.18)

Таким образом, прохождение сигнала с угловой модуляцией сопровождается амплитудной модуляцией (сомножитель ) и искажением закона изменения мгновенной фазы (слагаемое ) или частоты (слагаемое  в формуле (6.18)).

Более подробное рассмотрение показывает [1-3], что этот метод обеспечивает достаточную для практики точность при выполнении условий:

; ,

где  – период модулирующего (или видео-) сигнала;  – девиация частоты;  и - постоянная времени и половина полосы пропускания резонансной цепи.

6.3. Задачи

6.3.1. Воздействие импульсных сигналов на апериодические цепи

1. На вход цепи (рис. 6.3) подаётся прямоугольный импульс с амплитудой 20 В и длительностью 10^–4 с. Найдите сигнал на выходе цепи при Ом, Ф.

2. Решите задачу 1 при подаче на вход цепи треугольного импульса (рис. 6.4) с амплитудой 20 В и длительностью 200 мкс.

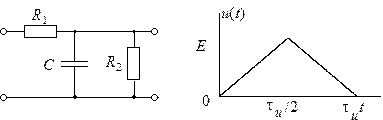
Рис. 6.3                                              Рис. 6.4

3. В момент времени  к электрической цепи, изображённой на рис. 6.5, подключается постоянная ЭДС  В. Найдите закон изменения напряжения на индуктивности. Параметры цепи:  Ом,  Ом,  Гн.

Рис. 6.5                                                     Рис. 6.6

4. Решите задачу 3 для случая, когда ЭДС на входе цепи  B.

5. Определите переходную характеристику активной цепи, изображённой на рис. 6.6.

6. Определите импульсную характеристику активной цепи, схема которой приведена на рис. 6.7.

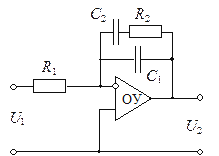
Рис. 6.7

6.3.2.  Интегрирование и дифференцирование импульсных сигналов

7. На вход интегрирующей RC цепочки подаётся периодическая последовательность прямоугольных импульсов амплитудой 20 В, длительностью 250 мкс и частотой следования 1 кГц.