![]()
Кафедра теоретических
основ радиотехники (ТОР)
Задание №3
Расчет LC генератора гармонических колебаний
Факультет: ФТФ Вариант 3
Группа: ФЛ-71 Подвариант 4
Студент: Духовникова Н.Ю.
Дата сдачи: 14.12.09
Преподаватель: Меренков В.М.
Новосибирск
2009
Рабочее задание
11.4 Расчет LC-генератора гармонических колебаний
|
Заданы тип схемы автогенератора гармонических колебаний (индуктивная трёхточка) и данные для расчёта.
Требуется:
а) начертить схему автогенератора;
б) аппроксимировать ВАХ НЭ;
в) рассчитать и
построить графически зависимость ![]() и
и ![]() , где I1
– амплитуда управляющего напряжения на входе НЭ;
, где I1
– амплитуда управляющего напряжения на входе НЭ;
г) определить
(графически или аналитически) для ![]() стационарные амплитуды
напряжения
стационарные амплитуды
напряжения ![]() на входе НЭ и первой гармоники тока I1ст на его входе; здесь S
- дифференциальная крутизна ВАХ в рабочей точке (при заданном U0);
на входе НЭ и первой гармоники тока I1ст на его входе; здесь S
- дифференциальная крутизна ВАХ в рабочей точке (при заданном U0);
д) рассчитать параметры контура автогенератора;
е) определить критический коэффициент βкр обратной связи и охарактеризовать режим возбуждения (мягкий или жёсткий); в случае жёсткого режима найти βкр1 и βкр2 ;
ж) рассчитать
коэффициент обратной связи и амплитуду выходного напряжения для стационарного
режима генерации.
Результаты выполнения задания
Исходные данные
Тип схемы – индуктивная трёхточка.
|
|
uз , В |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1.0 |
|
iс , мА |
0 |
0.1 |
0.5 |
1.3 |
3.0 |
6.0 |
11 |
17 |
25 |
36 |
65 |
U0 = 0.7 B, Zр = 200 Ом, ƒ0 = 3МГц, Q = 80
Требуется:
а) начертить схему автогенератора:
(а) Схема автогенератора
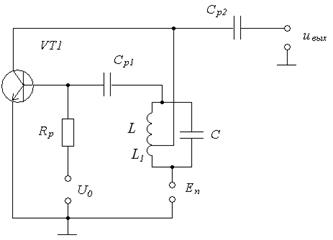
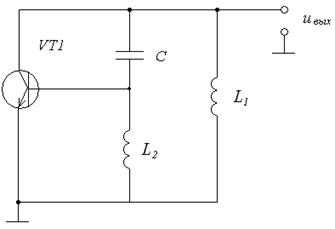
Рис.1. Схема принципиальная электрическая Рис.2. Схема эквивалентная автогенератора автогенератора б) аппроксимировать ВАХ НЭ:
(б) Аппроксимация ВАХ НЭ
Аппроксимируем ВАХ НЭ функцией вида I= a*exp{b*u}.
Определим коэффициенты аппроксимирующей функции
a=0.0008
b=4.33
Аппроксимирующая функция:i(u)= 0.0008*exp{4.33*u}.
(См. рис 3)
Дифференциальная крутизна ВАХ в рабочей точке (U0 = 0.7 B):
S=(i(u))1 в точке U0=0.7B
S=0.072
в) рассчитать и
построить графически зависимость ![]() и
и ![]() , где I1
– амплитуда управляющего напряжения на входе НЭ
, где I1
– амплитуда управляющего напряжения на входе НЭ
(в) Зависимости I1 = ƒ(Um) и Sср = φ(Um)
Колебательную характеристику построим с использованием метода трёх ординат, из которого следует, что искомая зависимость выглядит следующим образом.
|
|
uз , В |
0 |
0.05 |
0.1 |
0.15 |
0.2 |
0.25 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
|
iс , мА |
0 |
3 |
7 |
11 |
15 |
22.75 |
31 |
31.85 |
32.25 |
32.45 |
32.5 |
(См. рис 4)
Следующая зависимость находится тоже довольно просто.
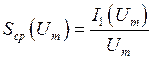
|
uз , В |
0.05 |
0.1 |
0.15 |
0.2 |
0.25 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
|
Sс , мА |
60 |
70 |
73.3 |
75 |
91 |
103.3 |
79.625 |
64.5 |
54.08 |
46.43 |
(См. рис 5)
г) определить (графически или
аналитически) для ![]() стационарные амплитуды напряжения
стационарные амплитуды напряжения
![]() на входе НЭ и первой гармоники тока I1ст на его входе; здесь S
- дифференциальная крутизна ВАХ в рабочей точке (при заданном U0)
на входе НЭ и первой гармоники тока I1ст на его входе; здесь S
- дифференциальная крутизна ВАХ в рабочей точке (при заданном U0)
(г) Стационарные амплитуды
Стационарные амплитуды (Uст и I1ст) определим графически из заданного условия:
![]() =0.072/1.3=0.055
=0.072/1.3=0.055
(См. рис 5)
Из рис.5 определяем, чтоUcт=0.13В
Определим стационарную амплитуду входного напряжения.
(См. рис 4)
|
На рис.4 прямая обратной связи проходит через точку (Uст , I1ст). Значение I1ст определяем по графику, зная Uст .
I1ст=9мА
д) рассчитать параметры контура автогенератора
(д) Определение параметров контура автогенератора
U0 = 0.7 B, Zр = 200 Ом, ƒ0 = 3МГц, Q = 80
Зная Zр, сразу найдём некоторые параметры.
ρ = Zр / Q= 200/80=2.5
ω0=2π*f0=6.28*3000000=1.885*107рад/c
C=1/ ω02*L= 1/ ω0* ρ=2.122* 10-8Ф
r = ρ2/ Zр=0.031
Для нахождения коэффициента неполного включения индуктивности p и индуктивностей L1 и L2 воспользуемся условиями самовозбуждения. Второе критическое условие:
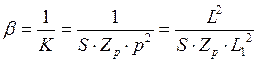 , где
, где 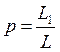
Но с другой стороны,
используя первое условие самовозбуждения (![]() ), устнавливаем:
), устнавливаем: 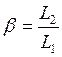 .
.
Сопоставляя полученные выражения, а также учитывая, что L = L1 + L2 , получаем систему:
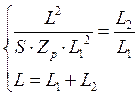 ;
; 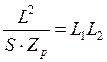 ;
; 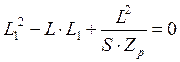
L2=L-L1
Полученное квадратное уравнение имеет два корня.
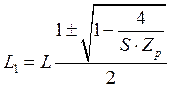
Получаем два набора параметров L1 , L2 и p.
1)L1’=1.192*10-7Гн L2’=1.341*10-8Гн p’= L1’/ L=0.899
2) L1’’=1.341*10-8Гн L2’’=1.192*10-7Гн p’’= L1’’/ L=0.101
|
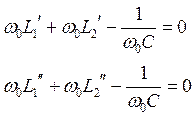
Обе проверки сходятся. Значит, оба набора параметров подходят для данного автогенератора. В дальнейшем мы ещё проверим этот вывод.
Но из малости p’’= L1’’/ L=0.101 мы видим,что этот набор параметров нам не подходит.
e) определить критический коэффициент βкр обратной связи и охарактеризовать режим возбуждения
(е) Критический режим
Критический коэффициент обратной связи:
βкр=1/(S* Zр* p2)=1/(200*0.07![]() )=0.086
)=0.086![]()
p’= L1’/ L=0.899 точка С- это точка срыва.
Um=0.3B
I1=17мА
Sср=103.3![]()
βкр2=1/(S* Zр)=1/(103.3![]() 200
200![]() =0.06
=0.06
Срыв происходит скачкообразно (жестко) при различных значениях β
режим жесткий точка В- это точка возникновения колебаний
Um=0.6B
I1=32.45мА
Sср=54.08![]()
βкр2=1/(S* Zр)=1/(103.3![]() 200
200![]() =0.114 ж) рассчитать коэффициент обратной
связи и амплитуду выходного напряжения для стационарного режима генерации.
=0.114 ж) рассчитать коэффициент обратной
связи и амплитуду выходного напряжения для стационарного режима генерации.
(ж) Стационарный режим
Коэффициент
обратной связи: β=1/(Scp cm* Zр* p2)=1/(200*0.055)=0.091
![]()
Найдём амплитуду выходного напряжения:
Zрэ’=p’2 *Zр=(0.899)2*200=161.64Ом U ‘вых m=I1(Ucm)* Zрэ’=1.454B
Итак, результирующие параметры контура:
L1=1.192*10-7Гн
L2=1.341*10-8Гн
p= L1’/ L=0.899
при этом U вых m=I1(Ucm)* Zрэ=1.454B
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.