Нелинейные преобразования сигналов, страница 4

При больших амплитудах  входного ВЧ колебания ВАХ НЭ можно аппроксимировать кусочно-линейной зависимостью, тогда

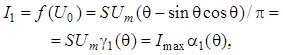                    (10.24)

где  – амплитуда импульсов тока, линейно зависящая от напряжения смещения . При изменении угла отсечки в пределах

                                     (10.25)

 и модуляционная характеристика

                      (10.26)

практически линейна, что свидетельствует о неискаженной АМ.

         

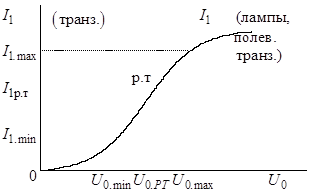
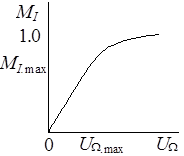
Рис. 10.7                                                          Рис. 10.8

Часто статическую модуляционную характеристику находят графоаналитически по известной ВАХ НЭ и заданной амплитуде входного сигнала , используя метод трех ординат.

Статическая модуляционная характеристика позволяет выбрать рабочий участок ВАХ НЭ, необходимый для неискаженной амплитудной модуляции (, ), и определить для этого участка:

1. Максимально возможный коэффициент АМ по току

.

2. Рабочее напряжение смещения (рабочую точку)

.

3. Максимальную амплитуду управляющего напряжения

.

Динамическая модуляционная характеристика (рис. 10.8) – это зависимость коэффициента модуляции M_I от амплитуды модулирующего сигнала  при постоянных смещении  и амплитуде ВЧ колебаний , т. е.

, , .                  (10.27)

Эта характеристика может быть рассчитана по статической модуляционной характеристике (если для обеих взяты одинаковые ) или на основе формул (10.16), (10.17). По формулам определяют зависимости максимального и минимального мгновенных значений тока первой гармоники (, ) от амплитуды модулирующего напряжения для известных (заданных) , . И затем

. (10.28)

   Детектирование АМС с использованием управляемых НЭ

Задача детектирования АМС заключается в перенесении спектра управляющего сигнала из области ВЧ в область НЧ (нелинейное преобразование) с последующим его выделением путем фильтрации ФНЧ (линейное преобразование).

Схема детектора показана на рис. 10.2, а, в. На управляющий вход НЭ подаются смещение и АМС

.                         (10.29)

Оператор  НП в общем случае описывают выражением (10.15). Для “слабого” сигнала, т. е. для сигнала, при котором в представлении оператора  можно ограничиться второй степенью полинома

,                          (10.30)

спектр тока вычисляют подстановкой (10.29) в (10.30). ФНЧ выделяет из этого спектра НЧ часть. Её можно рассматривать как медленно меняющуюся (по сравнению с АМС) постоянную составляющую .

.                 (10.31)

Ток детекторного эффекта обусловлен изменением амплитуды ВЧ колебаний

,                      (10.32)

где  – ток покоя в рабочей точке (, ).

Детекторная характеристика – зависимость тока детекторного эффекта от амплитуды ВЧ немодулированного колебания.

, , .                      (10.33)

Из (10.32) следует, что для “слабого” сигнала

                                    (10.34)

детекторная характеристика – квадратичная функция амплитуды. Такое детектирование называется квадратичным. Оно приводит к существенным нелинейным искажениям восстановленного модулирующего сигнала. В частности, при однотональной огибающей АМК

                             (10.35)

получим

.

Коэффициент нелинейных искажений (гармоник) согласно (10.2)

.

При ,  (25 %), что очень много.

При детектировании “сильного” сигнала ( велико) ВАХ НЭ аппроксимируется кусочно-линейной зависимостью (10.3) и ток детекторного эффекта

.

При  () имеем . Следовательно, детекторная характеристика

                                     (10.36)

линейна (рис. 10.9). Таким образом, при детектировании “сильного” сигнала имеет место “линейное” детектирование, т. е. детектирование без нелинейных искажений выделяемого НЧ сигнала. При этом НП работает в нелинейном режиме с отсечкой.

Напряжение на выходе детектора рассчитывается по формуле

.

В частном случае, при линейном детектировании, однотональном АМК на входе (10.35) и RC ФНЧ на выходе НП получим

,                         (10.37)