Нелинейные преобразования сигналов, страница 3

   Умножение частоты

Эта операция аналогична резонансному усилению (рис. 10.2, а, б). Разница заключается в том, что контур ЛП настраивается на -ю гармонику входного сигнала (). При этом будут справедливы основные формулы расчета нелинейного резонансного усилителя, в которых необходимо заменить напряжения, токи и параметры по первой гармонике соответствующими параметрами по -й гармонике.

Амплитуда напряжения на выходе умножителя рассчитывается по формуле

.                         (10.12)

Из (10.12) следует, что при ,  полностью определяется соответствующей функцией Берга , которая (рис.  П.3) достигает максимума при оптимальном угле отсечки

.

Если величина импульса тока  на выходе нелинейного элемента сохраняется постоянной, то для расчета  удобнее использовать коэффициенты . В этом случае

.                                     (10.13)

Коэффициент гармоник на выходе умножителя может быть рассчитан по формуле (10.10). При этом под корнем будут амплитуды всех гармоник, кроме -й, а в знаменателе амплитуда -й гармоники.

   Амплитудная модуляция управлением смещения на НЭ

Схема модулятора приведена на рис. 10.2, а, б. На управляющий вход НЭ подается высокочастотное (ВЧ) колебание , смещение  и модулирующий сигнал .  представляет собой медленную, по сравнению с ВЧ колебанием, функцию времени (т. е. всегда выполняется неравенство , где  – наивысшая частота в спектре сигнала ). Будем далее использовать в качестве простейшего модулирующего сигнала гармоническое колебание . Итак, на модулятор подается

,   (10.14)

где под  можно понимать медленно изменяющееся во времени по закону управляющего сигнала напряжение смещения НЭ , т. е.  = .

Представим оператор (·) НП (т. е. его ВАХ) степенным полиномом

                   (10.15)

Подставим напряжение (10.14) в (10.15). Выходной ток НП будет иметь сложный спектральный состав, содержащий частоты вида (8.24), где кроме гармоник несущего и управляющего сигналов появятся комбинационные составляющие вида

   …

Резонансный контур модулятора выделит из этого спектра составляющие с частотами, близкими к его резонансной частоте () (см. рис. 10.3).

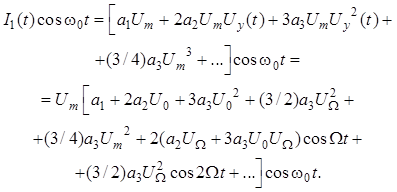        (10.16)

Для получения неискаженной модуляции порядок комбинационных составляющих  должен быть не более 2. Выберем на ВАХ нелинейного элемента участок, допускающий аппроксимацию не более чем квадратичным полиномом. Следовательно,  и амплитуда первой гармоники тока

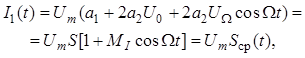                 (10.17)

где  – крутизна в рабочей точке ();  – глу-бина модуляции амплитуды тока первой гармоники

.                                   (10.18)

 – средняя крутизна (меняется во времени по закону модулирующего сигнала).

Коэффициент нелинейных искажений огибающей тока первой гармоники в соответствии с (10.2)

.                       (10.19)

Выходное напряжение модулятора рассчитывается по формуле

,              (10.20)

где , , , , , .

Таким образом, модулятор можно рассматривать как резонансный усилитель с управляемой крутизной. Изменение глубины модуляции напряжения  по сравнению с глубиной модуляции тока , а также запаздывание огибающей  на угол  по сравнению с огибающей тока – это линейные искажения. Они тем меньше, чем меньше добротность , т. е. шире полоса пропускания контура.

На практике рабочий участок ВАХ НЭ модулятора выбирают по статической модуляционной характеристике. Это зависимость амплитуды тока первой гармоники  НЭ или напряжения на выходе модулятора  от напряжения смещения  при подаче на вход гармонического несущего колебания с постоянной амплитудой  (рис. 10.7)

, , .                      (10.21)

Статическую модуляционную характеристику можно получить аналитически, например, подставив  в (10.16):

.           (10.22)

Для квадратичного участка ВАХ, когда , эта характеристика линейна

                                (10.23)

и, как уже отмечалось, нелинейные искажения огибающей отсутствуют.