Нелинейные преобразования сигналов, страница 2

где  – амплитуда – го вредного продукта (составляющей);  – амплитуда полезной составляющей.

В заключение отметим, что выше рассмотрена ситуация с “развязанными” НП и ЛП, когда отсутствует обратная реакция выходного напряжения на ток в НЭ.

И, наконец, следует подчеркнуть, что решение функционального уравнения (10.1) для задачи синтеза обычно намного сложнее, чем для задачи анализа. Серьезные трудности встречаются как в нахождении оператора , так и в его технической реализации. Задача синтеза доведена до конца лишь в немногих частных случаях (например, при умножении частоты).

   Нелинейное резонансное усиление

Одной из основных задач в радиотехнике является получение неискаженного сигнала заданной мощности при высоком КПД. Повышение КПД обеспечивается переводом НЭ (рис. 10.2, а) в принципиально нелинейный режим – с отсечкой тока. Для сохранения структуры сигнала используется нагрузка в виде резонансного контура (рис. 10.2, б), выделяющая из всего спектра тока составляющую гармонику  (при ). Пусть ВАХ НЭ аппроксимирована кусочно-ломаной линией (рис. 10.4).

.

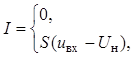
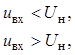
НЭ может работать в следующих режимах:

1) класс А, если ;

2) класс АВ, если ;

3) класс В, если ;

4) класс С, если .

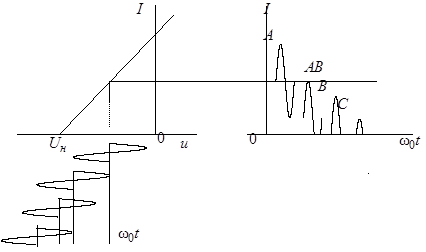
Рис. 10.4

Получение того или иного режима зависит от угла отсечки , который определяется , ,  (см. (8.17)).

Режим класса А – линейный режим работы НЭ. Форма и спектр сигнала на выходе НЭ соответствуют входным: .

В нелинейных режимах АВ, В, С импульсы выходного тока можно представить в виде

,      (10.4)

где  – постоянная составляющая;  – амплитуды гармоник на выходе НЭ, которые можно рассчитать по формулам прил. П.9. В частности, амплитуда тока первой гармоники (полезного продукта)

,          (10.5)

где , .

Основные характеристики и параметры резонансного усилителя:

1. Колебательная (амплитудная) характеристика (рис. 10.5, а):

 [или ], при

– зависимость амплитуды первой гармоники тока (напряжения) на выходе НЭ от амплитуды входного напряжения при постоянном смещении.

Для кусочно-линейной аппроксимации и аппроксимации степенным полиномом соответственно имеем:

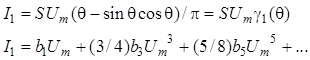
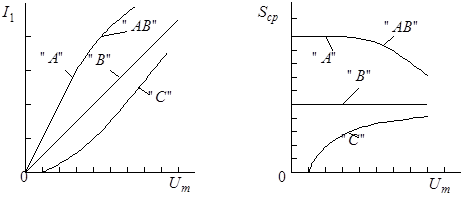
а                                                          б

Рис. 10.5

2. Средняя по первой гармонике крутизна НЭ (рис. 10.5, б)

.                                        (10.7)

3. Амплитуда выходного напряжения

,                                       (10.8)

где , , – внутреннее сопротивление НЭ.

4. Коэффициент усиления

.                      (10.9)

5. Коэффициент гармоник (используя формулу (10.2))

.                      (10.10)

6. Коэффициент полезного действия

,          (10.11)

где  – колебательная (полезная) мощность на выходе усилителя;  – мощность (постоянной составляющей), потребляемая от источника питания;  – коэффициент использования напряжения источника питания ().

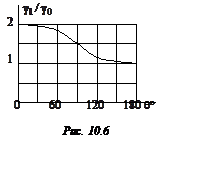
Из рис. 10.6 видно, что КПД резонансного усилителя при  стремится к 100 % (). Однако при этом  и . Для  (класс B), при ,  %. На основании (10.5) получим , т. е. колебательная характеристика линейна (рис. 10.5, а). Это важно при усилении АМК, которое будет происходить без искажения огибающей.

В случае, когда требуется получить максимум полезной мощности () на выходе усилителя, угол отсечки  доводят до , что соответствует максимуму функции , а это при  обеспечивает .

Тот факт, что в режимах с отсечкой при изменении  изменяется  и нарушается пропорциональность между амплитудами  и , свидетельствует о нелинейности преобразования. Однако сохранение формы колебаний на выходе по отношению ко входу позволяет говорить об устройстве как о линейной цепи и проводить расчет по первой гармонике выходного тока. Такой подход к анализу НЦ получил название квазилинейного метода. Он справедлив при высокой избирательности фильтра (, ).

Квазилинейный метод расчета может быть распространен на узкополосные () НЦ, возбуждаемые узкополосным сигналом (, где ).