Элементы цифровой обработки сигналов

Должен быть почитаем, как бог, тот, кто хорошо может определять и разделять.

Платон

 глава 14

   ЭЛЕМЕНТЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

14.1.  Изучаемые вопросы

Взаимосвязь аналоговых и дискретных сигналов. Линейные стационарные цепи. Импульсная характеристика. z-преобра-зование. Трансверсальные и рекурсивные цепи. Дискретное преобразование Фурье. [1, 12.5¼12.8,12.13; 2, 15.1¼15.6; 3, 10.1¼10.5; 25, 2.4, 2.5, 3.1¼3.4, 4.1¼4.5].

14.2. Краткие теоретические сведения

Аналоговый сигнал  со спектральной плотностью , такой, что

 при

может быть без потери информации заменен импульсным сигналом

,

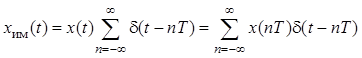где , или последовательностью отсчетов

; .

Спектральная плотность последовательности  определяется преобразованием Фурье

.

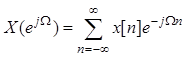Обратное преобразование Фурье

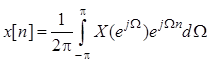
задает представление последовательности  в “сплошном” базисе комплексных экспоненциальных последовательностей

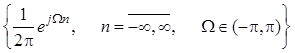
со спектральной плотностью амплитуд .

При  справедлива связь спектральных плотностей

.

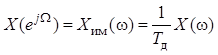Функция  периодична по  с периодом ; функция  периодична по  с периодом .

Линейная стационарная (инвариантная к сдвигу) цифровая цепь однозначно описывается последовательностью , называемой импульсной характеристикой (ИХ), причем если цепь устойчива, то ИХ абсолютно суммируема, т. е. .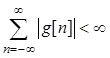

Импульсная характеристика представляет собой реакцию цифровой цепи на -последовательность, описываемую выражением

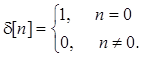
Последовательность “скачка”

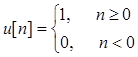
используется для описания последовательностей, равных нулю при отрицательных n (такие последовательности называются каузальными).

Выходная последовательность  связана с входной последовательностью  и импульсной характеристикой  выражением дискретной свертки

.

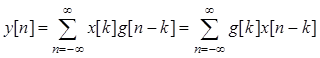Передаточная (системная) функция цепи определяется z-преобразованием импульсной характеристики

.

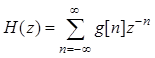Соотношением

связаны z-образы входной и выходной последовательностей и импульсной характеристики.

Обратное z-преобразование

                            ,

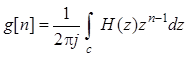где интеграл берется по контуру С, лежащему в области существования (сходимости) z-образа ; направление обхода положительно (против часовой стрелки).

Если z-образ имеет вид полинома

,

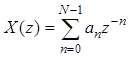то, очевидно, .

Если z-образ представляет собой дробно-рациональную функцию, т. е. частное двух полиномов

,

то при делении полиномов получается бесконечный ряд, причем коэффициенты ряда равны соответствующим отсчетам .

Основные свойства z-преобразования приведены в табл. 14.1.

Подстановка  в выражения z-образов входной и выходной последовательностей и импульсной характеристики дает соответственно спектральные плотности последовательностей и комплексную частотную характеристику (КЧХ):

;

;

,

так что

.

Цифровая каузальная цепь конечного порядка описывается разностным уравнением

,

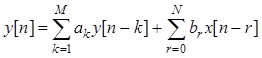где выходной отсчет не зависит от «будущих» значений входа и выхода.

Импульсная характеристика такой цепи  при .

Передаточная функция:

.

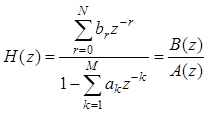Числитель дроби описывает трансверсальную, а знаменатель – рекурсивную части схемы, поэтому трансверсальная цепь умножает z-образ входной последовательности на полином , а рекурсивная – делит на полином .

Для последовательности ,  конечной длины  существует дискретное преобразование Фурье (ДПФ)

,

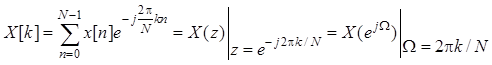определяющее  отсчетов ,  спектральной плотности или  отсчетов z-образа, взятых равномерно по окружности единичного радиуса в z-плоскости.

Обратное ДПФ

, .

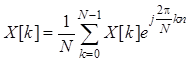Таблица 14.1

Последовательность	z-образ

14.3.  Задачи

1. Случайный сигнал имеет спектральную плотность мощности

,

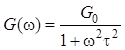где  – постоянная.

Определите частоту дискретизации так, чтобы на этой частоте СПМ составляла . Оцените мощность ошибки представления этого сигнала последовательностью. Как уменьшить эту ошибку?

2. Сигнал представляет собой импульс прямоугольной формы длительностью 10 мкс. Сигнал дискретизируется с шагом 1 мкс.

Запишите формулу для вычисления энергии ошибки дискретизации.

3. Цифровая цепь описывается разностным уравнением

.

Проверьте инвариантность к сдвигу.

4. Цифровая цепь описывается разностным уравнением

.

Проверьте инвариантность к сдвигу.

5. Цифровая цепь описывается разностным уравнением

.

Проверьте каузальность.

6. Цифровая цепь описывается разностным уравнением

.

Проверьте каузальность.

7. Реакция цифровой цепи  на воздействие  описывается выражением

.

Проверьте линейность цепи.

8. Реакция цифровой цепи  на воздействие  описывается выражением

.

Проверьте линейность цепи.