Основы вейвлет-преобразования сигналов

Я думаю, нет большей ненависти в мире,

чем ненависть невежд к знанию.

Галилео Галилей

 глава 16

   ОСНОВЫ ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ СИГНАЛОВ

16.1.  Изучаемые вопросы

Вейвлеты. Непрерывное и дискретное вейвлет-преобразование (ВП). Характерные отличия от преобразования Фурье. Признаки, свойства и примеры материнских вейвлетов. Свойства вейвлет-анализа и возможности ВП [31..34].

Указания. В конце настоящего раздела приведен обзор литературы по теории и практическому использованию ВП. Самые краткие общие сведения даны в учебнике [*.5], для более углубленного изучения возможностей ВП следует обратиться к одной из книг [*.1…*.4]. Подробные обзоры по ВП для тех, кто собирается применять это преобразование в практических расчетах и приложениях, приведены в работах [*.10, *.14]; при этом список литературы в [*.14] содержит 92 названия.

16.2. Краткие теоретические сведения

В последние годы возникло и успешно развивается новое и важное направление в теории и технике сигналов, получившее название вейвлет-преобразования (ВП), которое хорошо приспособлено для изучения структуры неоднородных процессов. Это направление еще не так хорошо известно широкому кругу отечественных исследователей и инженеров, поскольку применяется сравнительно недавно и математический аппарат его находится в стадии активной разработки.

Термин “вейвлет” (wavelet) ввели в своей статье Гроссман (Grossmann) и Морле (Morlet) в середине 80-х годов в связи с анализом свойств сейсмических и акустических сигналов. Их работа послужила началом интенсивного развития вейвлетов в последующее десятилетие рядом таких исследователей, как Добеши (Daubechies), Мейер (Meyer), Фарж (Farge), Чуи (Chui) и др.

Из анализа литературы и, в частности, приводимой в конце главы, следует, что ВП широко применяется для исследования нестационарных сигналов, неоднородных полей и изображений различной природы, распознавания образов и для решения многих других задач в радиотехнике, связи, электронике, ядерной физике, сейсмоакустике, метеорологии, медицине, биологии и других областях науки и техники.

Вопросы обработки сигналов в базисе вейвлетов лишь только начали освещаться в отечественной учебной литературе [*.2, *.4, *.6, *.7]. В то же время, в западных университетах читаются многочасовые курсы по теоретическим и практическим аспектам ВП, издаются монографии и уже много лет проводятся семинары и научные конференции.

Все изложенное выше послужило причиной включения основ ВП в программу курса и настоящей главы.

   Общая информация

Вейвлеты. Английское слово wavelet (от французского “ondelette”) дословно переводится как “короткая (маленькая) волна”. В различных переводах зарубежных статей на русский язык встречаются еще термины: “всплеск”, “всплесковая функция”, “маловолновая функция”, “волночка” и др.

ВП одномерного сигнала – это его представление в виде обобщенного ряда (1.13), (1.14) Фурье по системе базисных функций

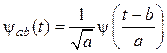,                                 (16.1)

сконструированных из материнского (исходного) вейвлета  за счет операций сдвига во времени () и изменения временного масштаба () (рис. 16.1). Множитель  обеспечивает независимость нормы этих функций от масштабирующего числа .

Малые значения  соответствуют мелкому масштабу  или высоким частотам (), большие параметры  – крупному масштабу , т. е. растяжению материнского вейвлета  

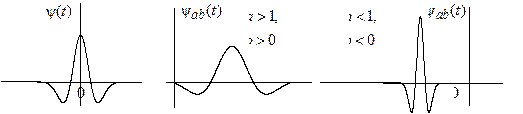
Рис. 16.1

и сжатию его спектра. При этом в соответствии с принципом неопределенности произведение эффективной длительности () и эффективной ширины спектра () функции  (площадь прямоугольников на рис. 16.2) остается неизменной. Кроме того, из-за масштабирования и временного сдвига () сохраняется относительная “плотность” расположения базисных функций по оси .

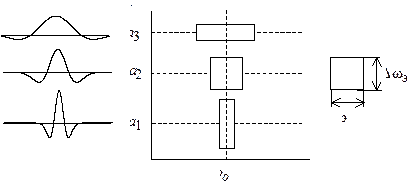
Рис. 16.2

Непрерывное (интегральное) вейвлет-преобразование (НВП или СWT – continuous wavelet transform). Сконструируем базис функционального пространства ( с помощью непрерывных масштабных преобразований и переносов материнского вейвлета  с произвольными значениями базисных параметров  и  в формуле (16.1).

Тогда по определению прямое (анализ) и обратное (синтез) HВП (т. е. ПНВП и ОНВП) сигнала  запишутся:

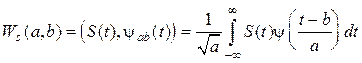,             (16.2)

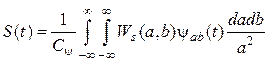,                      (16.3)

где – нормирующий коэффициент

,

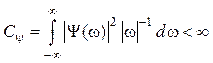 – фурье-преобразование вейвлета . Для ортонормированных вейвлетов = 1.

Из (16.2) следует, что вейвлет-спектр  (wavelet spectrum или time-scale-spectrum – масштабно-временной спектр) в отличие от фурье-спектра (single spectrum) является функцией двух аргументов: первый аргумент (временной масштаб) аналогичен периоду осцилляций, т. е. обратен частоте, а второй  – аналогичен смещению сигнала по оси времени.

Следует отметить, что  характеризует временную зависимость (для временного масштаба ), тогда как зависимости  можно поставить в соответствие частотную зависимость (для смещения ).

Если исследуемый сигнал  представляет собой одиночный импульс длительностью , сосредоточенный в окрестности , то его вейвлет-спектр будет иметь наибольшее значение в окрестности точки с координатами , .

Способы представления (визуализации)  могут быть различными. Спектр  является поверхностью в трехмерном пространстве (см. рис.  П.8). Однако часто вместо изображения поверхности представляют её проекцию на плоскость  с изоуровнями (рис.  П.9), позволяющими проследить изменение интенсивности амплитуд ВП на разных масштабах () и во времени (). Кроме того, изображают картины линий локальных экстремумов этих поверхностей, так называемый скелетон (sceleton), который выявляет структуру анализируемого сигнала.

Разложение сигнала в ряд по вейвлетам. При непрерывном изменении параметров  и b для расчета вейвлет-спектра необходимы большие вычислительные затраты. Множество функций  избыточно. Необходима дискретизация этих параметров при сохранении возможности восстановления сигнала из его преобразования. Дискретизация как правило осуществляется через степени двойки [*.1, *.2, *.4]:

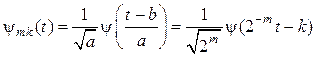, , ,    (16.4)

где  и – целые числа. В этом случае плоскость  превращается в соответствующую сетку .

Рис. 16.3 на примере вейвлета Хаара иллюстрирует дискретизацию : для различных значений  ширина  различна и выбор  гарантирует, что растянутые вейвлеты на уровне  “покрывают” ось времени так же, как это делают исходные вейвлеты на уровне .

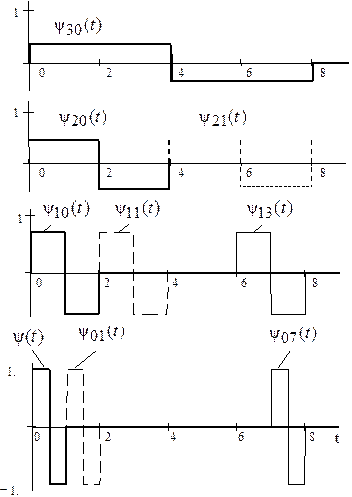
Рис. 16.3

Прямое и обратное дискретные вейвлет-преобразования (ДВП) непрерывных сигналов запишутся в виде:

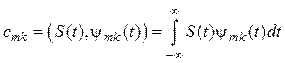,                     (16.5)

.                                  (16.6)

Проводя аналогию с преобразованием Фурье, коэффициенты  разложения (16.5) можно определить через НВП

.                                  (16.7)

Обращаясь к (16.5) и (16.7), видим, что вейвлет-спектр  можно представить как “лес” из вертикальных отрезков, размещенных над - плоскостью (сеткой); при этом целочисленные координаты  и  указывают соответственно на скорость изменения сигнала и положение вдоль оси времени.

Из (16.6) следует, что сигнал  может быть представлен суммой “вейвлетных волн” с коэффициентами . Формально обобщенный ряд Фурье (16.6) отличается от рассмотренного ранее ряда (1.13) тем, что суммирование проводится не по одному, а по двум индексам. Однако это несущественно, так как обе системы индексации принадлежат одному классу бесконечных счетных множеств.

Примечания. 1. Статьи, касающиеся практического использования ВП, содержат в основной своей массе результаты компьютерных расчетов, в которых использовано дискретное вейвлет-преобразование (ДВП). При этом не только параметры  и b, но и сигналы также дискретизируются во времени. Если число отсчетов составляет , то максимальное значение  в формулах (16.4) будет равно . Наибольшее значение  для текущего  определяется: . В частности, для  (т. е.  число сдвигов  базисного вейвлета составит ; с каждым последующим значением (1, 2, …) вейвлет расширяется в два раза, а число сдвигов  уменьшается в два раза. Для максимального значения , равного , , т. е. один вейвлет  “накрывает” весь интервал сигнала (рис. 16.3; ).

2. В некоторых публикациях параметры ,  и базисные функции задаются