В одном мгновенье – видеть вечность,
Огромный мир – в зерне песка,
В единой горсти – бесконечность
И небо – в чашечке цветка.
У. Блейк
 глава13
глава13
ПРИНЦИП УСИЛЕНИЯ И ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ В ПАРАМЕТРИЧЕСКОМ КОНТУРЕ
13.1. Изучаемые вопросы
Энергетические соотношения в цепи с параметрическими реактивными элементами. Вносимые сопротивления в режимах синхронной и асинхронной накачки. Физические процессы при параметрическом усилении колебаний. Параметрические усилители, их достоинства и области применения [1, 10.5¼10.7; 2, 12.2, 12.3; 21, 4.1¼4.4].
Параметрическое возбуждение колебаний, дифференциальное уравнение контура с параметрической реактивностью. Результаты решения уравнения Матье, физические процессы при возбуждении параметрического контура. Стационарный режим генерации, нелинейные явления (механизмы) ограничения амплитуды. Мягкий и жесткий режимы самовозбуждения. Параметрические генераторы [1, 10.8; 2, 12.2; 22, 1¼3].
Баланс мощностей в многоконтурных параметрических системах. Уравнения Мэнли-Роу [2, 12.3].
Указания. Большинство изучаемых вопросов нашло должное отражение в [21, 22], где достаточно подробно изложена физическая сторона рассматриваемых явлений и процессов при сохранении строгости математического изложения.
По ряду изучаемых вопросов в руководствах [5, 6] приведены примеры и задачи с методическими указаниями, решениями и ответами.
13.2. КРАТКИЕ Теоретические сведения
Вносимое сопротивление
Известно [1, 2, 21, 22], что при периодическом изменении реактивного
параметра (![]() или
или ![]() )
радиотехнической цепи в ней меняются энергетические соотношения. Энергия
периодически либо вносится («накачивается») в цепь от генератора накачки, изменяющего
параметр, либо отбирается («откачивается») из цепи. Эти процессы можно
рассматривать как внесение в цепь сопротивления
)
радиотехнической цепи в ней меняются энергетические соотношения. Энергия
периодически либо вносится («накачивается») в цепь от генератора накачки, изменяющего
параметр, либо отбирается («откачивается») из цепи. Эти процессы можно
рассматривать как внесение в цепь сопротивления ![]() ; при
этом
; при
этом ![]() , когда в цепь вводится дополнительная энергия,
и
, когда в цепь вводится дополнительная энергия,
и ![]() , когда потери в цепи возрастают. Тогда
эквивалентная схема цепи с периодически
изменяющейся емкостью
, когда потери в цепи возрастают. Тогда
эквивалентная схема цепи с периодически
изменяющейся емкостью ![]() или индуктивностью
или индуктивностью ![]() представляется
в виде цепи с постоянной емкостью
представляется
в виде цепи с постоянной емкостью ![]() или индуктивностью
или индуктивностью ![]() и активным сопротивлением
и активным сопротивлением ![]() .
.
На рис. 13.1 показана схема контура с периодически изменяющейся емкостью (а) и его эквивалентная схема (б). На рис. 13.2 даны пояснительные временные диаграммы.
Изменение энергетических соотношений описывается простыми
выражениями: ![]() ,
, ![]() .
Уменьшение емкости в момент
.
Уменьшение емкости в момент ![]() на
на ![]() , когда
, когда ![]() ,
приведет к максимальному приращению энергии в цепи
,
приведет к максимальному приращению энергии в цепи ![]() и
увеличению напряжения на
и
увеличению напряжения на ![]() . Через полпериода (
. Через полпериода (![]() ) уменьшение параметра снова увеличит
энергию и напряжение и т. д.
) уменьшение параметра снова увеличит
энергию и напряжение и т. д.
Режим, при котором параметр меняется с двойной частотой входного
сигнала ![]() , называется синхронным. Вносимое сопротивление
описывается выражением [21].
, называется синхронным. Вносимое сопротивление
описывается выражением [21].
![]() ,
(13.1)
,
(13.1)
где ![]() – сопротивление параметрического
элемента на частоте входного сигнала,
– сопротивление параметрического
элемента на частоте входного сигнала, ![]() –
коэффициент вариации (глубина модуляции) параметра,
–
коэффициент вариации (глубина модуляции) параметра, ![]() –
начальный фазовый сдвиг, а
–
начальный фазовый сдвиг, а ![]() – временной сдвиг
сигнала (рис. 13.2, б); если наибольшая скорость уменьшения емкости
соответствует максимуму заряда на конденсаторе, т. е.
– временной сдвиг
сигнала (рис. 13.2, б); если наибольшая скорость уменьшения емкости
соответствует максимуму заряда на конденсаторе, т. е.
![]() , (13.2)
, (13.2)
то ![]() ,
, ![]() и
вносимое сопротивление максимально
и
вносимое сопротивление максимально ![]() .
.
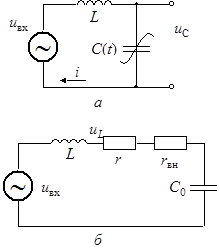
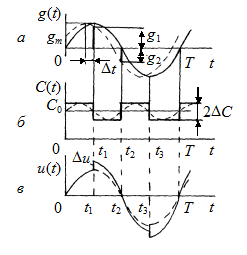
Рис. 13.1 Рис. 13.2
Коэффициент пропорциональности ![]() в формуле
(13.1) зависит от закона изменения параметра. Для прямоугольного (скачкообразного)
и гармонического законов соответственно имеем
в формуле
(13.1) зависит от закона изменения параметра. Для прямоугольного (скачкообразного)
и гармонического законов соответственно имеем
![]() ;
; ![]() . (13.3)
. (13.3)
При ![]() (
(![]() ) имеет
место асинхронный режим накачки. В этом случае фазовый сдвиг
) имеет
место асинхронный режим накачки. В этом случае фазовый сдвиг ![]() (или
(или ![]() ) не
остается постоянным, а изменяется со временем, т. е.
) не
остается постоянным, а изменяется со временем, т. е. ![]() .
Поэтому вносимое сопротивление, определяемое по формуле [21],
.
Поэтому вносимое сопротивление, определяемое по формуле [21],
![]() , (13.4)
, (13.4)
где ![]() , изменяется во времени с частотой
, изменяется во времени с частотой
![]() ; при этом изменяется как величина, так и
знак вносимого сопротивления. В частном случае, когда
; при этом изменяется как величина, так и
знак вносимого сопротивления. В частном случае, когда ![]() и
и
![]() , формула (13.4) превращается в формулу
(13.1).
, формула (13.4) превращается в формулу
(13.1).
Параметрическое усиление
Если выходное напряжение снимать с одного из реактивных элементов
контура (рис. 13.1, а) то на резонансной частоте (![]() ,
, ![]() ,
, ![]() ) коэффициент передачи
) коэффициент передачи
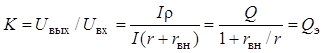 (13.5)
(13.5)
будет зависеть от величины и знака вносимого сопротивления.
Коэффициент усиления ![]() , показывающий, во
сколько раз увеличивается коэффициент передачи параметрического контура по
сравнению с обычным, определяется как
, показывающий, во
сколько раз увеличивается коэффициент передачи параметрического контура по
сравнению с обычным, определяется как
![]() . (13.6)
. (13.6)
Подставляя в (13.6) значение ![]() из
(13.1) и (13.4), получаем для синхронного и асинхронного режимов накачки
из
(13.1) и (13.4), получаем для синхронного и асинхронного режимов накачки
![]() ; (13.7)
; (13.7)
![]() . (13.8)
. (13.8)
Недостаток асинхронного режима – изменение коэффициента
усиления во времени (с частотой ![]() ).
).
Так как вносимое сопротивление зависит от ![]() ,
то и коэффициенты передачи
,
то и коэффициенты передачи ![]() и усиления
и усиления ![]() зависят от
зависят от ![]() .
Поэтому параметрическое усиление обладает свойством фазовой избирательности.
В синфазном режиме (
.
Поэтому параметрическое усиление обладает свойством фазовой избирательности.
В синфазном режиме (![]() и
и ![]() )
коэффициент усиления максимален
)
коэффициент усиления максимален
![]() . (13.9)
. (13.9)
Из соображений устойчивости необходимо, чтобы ![]() . Поэтому глубина модуляции параметра не
должна превышать критического значения
. Поэтому глубина модуляции параметра не
должна превышать критического значения
![]() . (13.10)
. (13.10)
На рис. 13.3, а дана схема параллельного параметрического
контура, подключенного к источнику тока с проводимостью ![]() ,
а на рис. 13.3, б – схема замещения, где
,
а на рис. 13.3, б – схема замещения, где ![]() –
проводимость эквивалентной нагрузки, включающей в себя как проводимость контура
–
проводимость эквивалентной нагрузки, включающей в себя как проводимость контура
![]() , так и проводимость собственно нагрузки
, так и проводимость собственно нагрузки ![]() ,
, ![]() – вносимая
проводимость
– вносимая
проводимость
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.