Принцип усиления и возбуждения колебаний в параметрическом контуре, страница 2

,                               (13.11)

в случае синхронной накачки равная

.                             (13.12)

а                                                          б

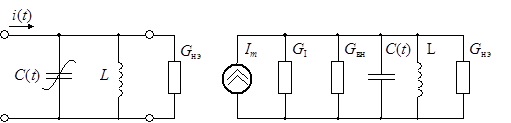
Рис. 13.3

Напряжение на нагрузке и рассеиваемая в ней мощность равны:

                          ;

                     .                      (13.13)

При отсутствии параметрической модуляции (т. е. при ) имеем

,

,

следовательно, коэффициенты усиления напряжения и мощности

;

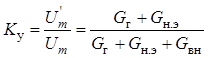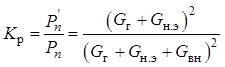.                         (13.14)

На рис. 13.4 показана схема одного из практических вариантов одноконтурного параметрического усилителя на варикапе, где  – собственно параметрический контур. Для согласования источника сигнала используется частичное включение контура. Выходное напряжение по той же причине может сниматься не со всей катушки (выводы 1-4), а только с ее части (выводы 1-3).

t

DС

С(t)

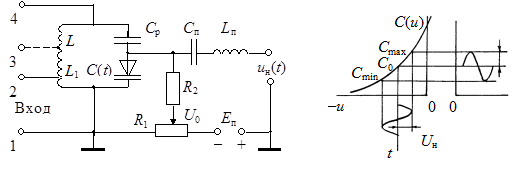
Рис. 13.4

   Параметрическая генерация

Общая теория возбуждения параметрического контура основана на исследовании решений дифференциального уравнения, описывающего физические процессы в контуре [22].

Условие самовозбуждения параметрического контура

 и .                             (13.15)

Установление колебаний в реальном параметрическом контуре, как и в автогенераторе любого типа, происходит вследствие нелинейных механизмов (явлений). При этом во время переходного процесса характеристики автоколебательной цепи изменяются до тех пор, пока не наступит энергетический баланс, т. е. пока вносимая в контур мощность  (сопротивление  или проводимость ) не станет равной мощности потерь  ( или )

, , .                         (13.16)

В контуре, использующем варикап в качестве переменной емкости, основными механизмами ограничения амплитуды являются два [22]: диссипативный и расстроечный.

Расстроечный механизм обусловлен нелинейностью зависимости  (рис. 13.5, а). С ростом амплитуды  генерируемых колебаний и, следовательно, амплитуды напряжения на p-n-переходе варикапа увеличивается среднее значение емкости , уменьшается характеристическое сопротивление и резонансная частота контура. В результате уменьшается вносимое сопротивление.

При диссипативном механизме ограничение амплитуды происходит за счет увеличения потерь в контуре, что обусловлено нелинейностью вольт-амперной характеристики  p-n-перехода (рис. 13.5, а). С ростом амплитуды генерируемых колебаний увеличивается , уменьшается  и, следовательно, возрастает последовательное сопротивление  и суммарное сопротивление потерь (рис. 13.6, а)

.                                    (13.17)

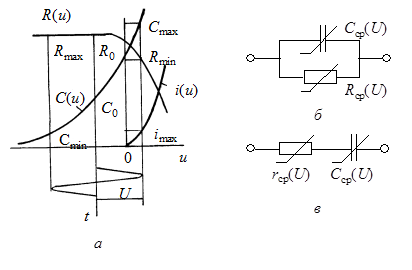
Рис. 13.5

С учетом изложенного эквивалентная схема генератора, представленная на рис. 13.6, а, содержит активные сопротивления , , . От сопротивлений можно перейти к проводимостям , ,  (рис. 13.6, б).

Практические схемы параметрических генераторов (параметронов) отличаются от изображенных на рис. 13.6 и построены по балансному принципу (рис. 13.7), что обеспечивает подавление на выходе генератора колебания с частотой накачки.

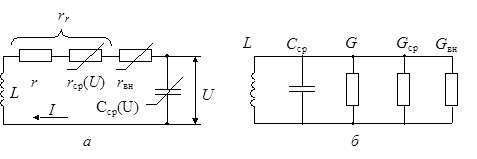
Рис. 13.6

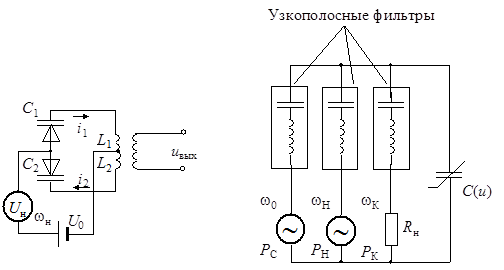
Рис. 13.7                                                                           Рис. 13.8

   Баланс мощностей в многоконтурных параметрических схемах

В схеме, изображенной на рис. 13.8, параллельно конденсатору  включены три цепи, две из которых имеют источники сигнала и накачки с соответствующими узкополосными фильтрами, пропускающими колебания с частотами  и . Третья цепь – это сопротивление нагрузки и контур, настроенный на комбинационную частоту

,                                   (13.18)

где  и  – целые числа. Ток комбинационной частоты может замыкаться только через цепь этого контура и выделять в нагрузке  некоторую мощность .

Для рассматриваемой автономной системы в соответствии с законом сохранения энергии для средних мощностей в цепях имеем

.

Это равенство должно выполняться тождественно для любых  и , что имеет место лишь при

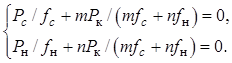                         (13.19)

Уравнения (13.19), называемые уравнениями Мэнли-Роу, определяют перераспределение мощностей в многоканальной системе.