В действительности все не так,
как на самом деле.
Станислав Ежи Лец
 глава 7
глава 7
ПРОХОЖДЕНИЕ СЛУЧАЙНЫХ ПРОЦЕССОВ ЧЕРЕЗ ЛИНЕЙНЫЕ РАДИОЦЕПИ
7.1. Изучаемые вопросы
Спектральная плотность мощности (СПМ) и корреляционная функция стационарного случайного процесса на выходе линейной цепи. Средняя мощность колебаний на выходе. Корреляция между входным и выходным процессами в установившемся режиме. Воздействие белого шума на линейные цепи. Нормализация случайного процесса в линейной цепи. Дифференцирование и интегрирование случайных процессов. Распределение огибающей гауссова процесса и смеси гармонического сигнала с гауссовым шумом [1, гл.7, 4.6; 2, гл.10, 7.3; 3, гл.19].
Указания. Вопросы анализа случайных процессов (СП) в линейных цепях подробно рассмотрены в [1, 3,11]. Руководства [5…9] содержат большое количество задач с комментариями и решениями.
Большинство встречающихся на практике задач можно разделить на два класса. К первому относят задачи, связанные с определением динамических характеристик выходного процесса (его автокорреляционной функции и спектральной плотности мощности), а также взаимной корреляции случайных процессов (на входе и выходе цепи, на выходах различных цепей при общем входном воздействии и т. п.). Задачи второго класса посвящаются определению плотностей распределения вероятностей мгновенных значений выходного процесса.
В настоящей главе будут рассмотрены задачи, связанные с анализом
случайных процессов на выходах линейных стационарных цепей, когда на входы
цепей воздействуют стационарные в широком смысле случайные процессы. При этом
обычно предполагается, что переходные процессы в цепи закончились (или, что
эквивалентно, случайный процесс присутствует на входе цепи с момента времени ![]() ).
).
Задачи, связанные с плотностью распределения вероятностей мгновенных значений СП, будут рассматриваться лишь для частного, хотя и важного, случая гауссова процесса.
7.2. Краткие теоретические сведения
Если нестационарность СП ![]() выражается лишь в
непостоянстве математического ожидания
выражается лишь в
непостоянстве математического ожидания ![]() , то
можно, имея в виду принцип суперпозиции, анализировать отдельно прохождение через
линейную цепь детерминированной функции
, то
можно, имея в виду принцип суперпозиции, анализировать отдельно прохождение через
линейную цепь детерминированной функции ![]() и флюктуационной
составляющей случайного процесса. При этом
и флюктуационной
составляющей случайного процесса. При этом
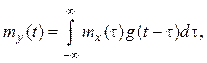
где ![]() – математическое ожидание
выходного процесса
– математическое ожидание
выходного процесса ![]() ;
; ![]() –
импульсная характеристика цепи.
–
импульсная характеристика цепи.
Если процесс ![]() на входе цепи стационарен
в широком смысле с автокорреляционной функцией
на входе цепи стационарен
в широком смысле с автокорреляционной функцией ![]() , то
автокорреляционная функция выходного процесса
, то
автокорреляционная функция выходного процесса ![]()
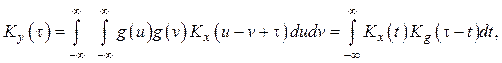
где 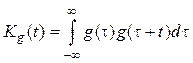 – автокорреляционная функция импульсной
характеристики цепи.
– автокорреляционная функция импульсной
характеристики цепи.
Взаимная корреляционная функция входного и выходного процессов
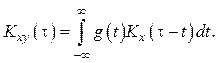
Если один и тот же СП ![]() воздействует на входы
цепей с импульсными характеристиками
воздействует на входы
цепей с импульсными характеристиками ![]() и
и ![]() , то для процессов
, то для процессов ![]() и
и
![]() на их выходах взаимная корреляционная
функция
на их выходах взаимная корреляционная
функция
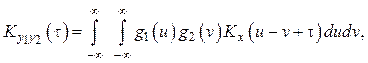
Учитывая, что динамические свойства стационарного в широком смысле
процесса могут быть описаны как корреляционной функцией, так и спектральной
плотностью мощности, можно анализ прохождения таких процессов через линейные
цепи проводить в частотной области. Так, СПМ процесса ![]()
![]()
где ![]() – СПМ процесса
– СПМ процесса ![]() ;
; ![]() –
передаточная функция цепи.
–
передаточная функция цепи.
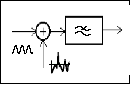
Целесообразный метод расчёта спектрально-корреляционных характеристик СП в линейной цепи с минимальным числом интегральных преобразований можно выбрать при помощи схемы (графа), показанной на рис. 7.1.
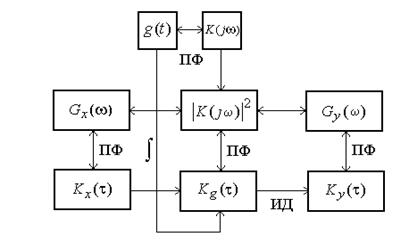
Рис. 7.1
Взаимная СПМ входного и выходного процессов
![]()
а взаимная СПМ процессов ![]() и
и ![]() на выходах двух цепей, возбуждаемых одним
и тем же процессом
на выходах двух цепей, возбуждаемых одним
и тем же процессом ![]() ,
,
![]()
Напомним, что СПМ стационарного в широком смысле СП связана с его автокорреляционной функцией парой преобразований Фурье (теорема Винера-Хинчина). То же справедливо для взаимных корреляционных функций и взаимных СПМ.
Числовыми характеристиками, дающими некоторое представление о динамике случайного процесса, являются эффективная ширина спектра и интервал корреляции.
Иногда употребляют числовую характеристику
цепи, называемую шумовой полосой. По определению шумовая полоса линейной цепи с
передаточной функцией ![]() – это полоса пропускания такого
идеального ФНЧ (с прямоугольной АЧХ), который при воздействии белого шума
обеспечивает такую же дисперсию выходного процесса, как и данная цепь
– это полоса пропускания такого
идеального ФНЧ (с прямоугольной АЧХ), который при воздействии белого шума
обеспечивает такую же дисперсию выходного процесса, как и данная цепь
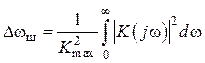 ,
,
где ![]() –
максимальное значение АЧХ цепи.
–
максимальное значение АЧХ цепи.
Анализ распределения вероятностей выходного СП в общем случае весьма сложен. Достаточно просто эта задача решается в случае узкополосной цепи. Тогда при любом распределении входного СП распределение вероятностей выходного процесса сходится к нормальному и гауссово приближение тем точнее, чем более справедливо допущение о некоррелированности значений входного СП (или чем ближе СПМ входного процесса к константе в полосе пропускания цепи). Если же входной процесс гауссов, то и СП на выходе линейной цепи гауссов независимо от формы СПМ и характеристик цепи. В указанных случаях для нахождения полного вероятностного описания СП на выходе цепи достаточно найти математическое ожидание и автокорреляционную функцию выходного процесса.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.