Прохождение случайных процессов через линейные радиоцепи, страница 3

Найдите по графикам распределения Рэлея-Райса [2] такой пороговый уровень для последетекторного обнаружения, при котором сумма вероятностей указанных ошибок минимальна (примите амплитуду сигнала равной 5 В, СКО шума на входе детектора 1 В).

24. При тех же параметрах сигнала и шума найдите оптимальный (в смысле минимума суммарной вероятности ошибки) порог в предположении, что шум описывается нормальным распределением с нулевым средним, а смесь сигнала с шумом имеет математическое ожидание, равное амплитуде сигнала (эта ситуация соответствует обнаружителю на выходе синхронного детектора). Оцените изменение суммарной вероятности ошибки.

7.4.         Контрольное задание

7.4.1.  Воздействие стационарного случайного сигнала на линейную радиоцепь

На линейную цепь с коэффициентом передачи  или импульсной характеристикой  действует стационарный случайный процесс с известной СПМ  или корреляционной функцией  (см. табл. 7.1 и 7.2).

В табл. 7.1 и 7.2 приняты следующие обозначения: G₀ – спектральная плотность мощности “белого” шума на входе;  – дисперсия входного случайного процесса;  – постоянная, характеризующая скорость убывания корреляционной функции;  – временной сдвиг; K₀ – наибольшее значение коэффициента передачи линейной цепи; t_ф – постоянная времени линейной цепи (фильтра), при этом ; – центральная частота спектра случайного процесса или радиоцепи.

Требуется:

а) определить спектральную плотность мощности на выходе  и построить нормированные графики ,  и ; б) вычислить полосу пропускания цепи и ширину спектра на уровне 0.5 (по формулам и графикам п.“а”);

в) найти шумовую полосу линейной цепи и эффективную ширину спектра входного и выходного процессов;

г) рассчитать дисперсию  выходного процесса;

д) определить автокорреляционную функцию на выходе  и построить нормированный график ;

е) вычислить интервал корреляции  выходного процесса.

    Методические указания

При решении задачи следует воспользоваться теоремой Винера-Хинчина и спектральным методом анализа прохождения случайных процессов через линейные цепи. Нахождение преобразований Фурье и определение дисперсии можно проводить с использованием справочного материала (см. прил. П.3 [1]) или теоремы о вычетах.

Для вариантов 0 и 2 значение  из табл. 7.2 не используйте, так как в этом случае . Для вариантов 5, 6, 8 и 9 следует считать, что . При построении корреляционной функции на выходе линейной цепи в вариантах 1, 4, можно считать, что .

Таблица 7.1

Окончание табл. 7.1

Таблица 7.2

7.4.2.  Прохождение сигнала и шума через линейную радиоцепь

На вход цепи, показанной на рис. 7.2, воздействует стационарный белый шум  с двусторонней спектральной плотностью мощности .

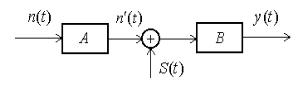
Рис. 7.2

Устройство А представляет собой фильтр, формирующий процесс  со спектральной плотностью мощности требуемого вида. В сумматоре этот процесс складывается с детерминированным сигналом  и поступает на фильтр В.

Вид фильтров А и В определяется номером варианта (табл. 5.1 и 5.2), параметры – номером подварианта (табл. 5.3).

Требуется:

а) найти СПМ процесса . Определить параметр , при котором процесс  имеет единичную дисперсию;

б) определить АКФ  процесса ;

в) вычислить эффективную ширину спектра  и интервал корреляции  процесса ;

г) рассчитать эффективную ширину спектра  и интервал корреляции  шумовой составляющей процесса ;

д) определить отношение сигнал/шум на выходе фильтра В.

При выполнении п. 5 в качестве  следует рассмотреть гармонический сигнал с единичной амплитудой и частотой, равной 3/4 эффективной ширины спектра шума на выходе фильтра В.