Министерство образования Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
_____________________________________________________________________
Кафедра теоретических основ радиотехники (ТОР)
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ
ЗАДАНИЕ N 2
Вариант N 5
Подвариант N 4
Факультет РЭФ
Группа РТ- 5 - 23
Студент: Ковалева Т.С.
Дата сдачи « 29» октября 2004 г.
Преподаватель:
Новосибирск, 2004
10.4.1. Нелинейное резонансное усиление сигналов и умножение частоты.
Задание:
Нелинейный
резонансный усилитель или умножитель частоты собран по схеме. На вход схемы
поступает напряжение ![]() , В. В качестве выходной нагрузки
включен резонансный контур с wрез = w0 для нелинейного усилителя и wрез = nw0 для
умножителя частоты.
, В. В качестве выходной нагрузки
включен резонансный контур с wрез = w0 для нелинейного усилителя и wрез = nw0 для
умножителя частоты.
Исходные данные:
|
S, мА/В |
Uн, В |
U0, В |
Um, В |
n |
L, мГн |
r, Ом |
wрез, рад/с |
p |
|
100 |
-1 |
-2 |
2 |
3 |
1 |
40 |
1*106 |
0.15 |
Требуется:
а) построить ВАХ заданного НЭ, рассчитать коэффициенты аппроксимирующей функции, построить эту функцию на одном графике с ВАХ;
б) рассчитать и построить колебательную характеристику для нелинейного усилителя;
в) рассчитать и построить спектр тока НЭ вплоть до четвертой гармоники включительно;
г) определить амплитуду рабочей гармоники на выходе НЭ Uвых и на колебательном контуре Uк;
д) рассчитать мощность P0, поступающую от источника питания, мощность Pвых, выделяемую в нагрузке на рабочей частоте, мощность Pк.т., выделяемую на коллекторе в виде тепла и КПД усилителя h= PП/P0. Напряжение питания Eп = 24 В.
а) Аппроксимирующая функция заданного НЭ:
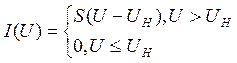
|
|
рис.1. Аппроксимация и ВАХ НЭ.
б) колебательная характеристика:
Рассчитаем колебательную характеристику. Для этого запишем формулу для определения угла отсечки при различных амплитудах входного сигнала:
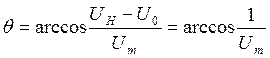
Запишем формулу коэффициента первой гармоники функции Берга:
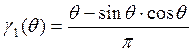
Запишем формулу зависимости амплитуды первой гармоники тока от амплитуды входного напряжения:
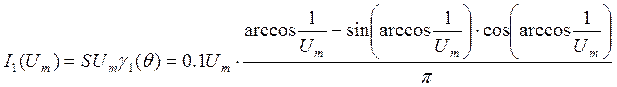
Построим колебательную характеристику:
|
|
рис.2. Колебательная характеристика.
в) рассчитаем и построим спектр тока НЭ:
![]()
Найдем угол отсечки:
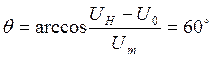
![]()
![]()
![]()
![]()
![]()
Так
как wрез = 2w0, то 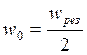 =
=![]() рад/с
рад/с
|
|
рис.3. Спектр тока НЭ.
г) амплитуда рабочей гармоники на выходе НЭ:
Напряжение на выходе НЭ – это есть напряжение на коллекторе.
Найдем емкость конденсатора в колебательном контуре:
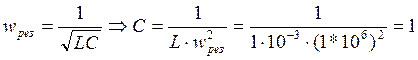 нФ
нФ
Найдем удельное сопротивление:
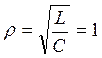 КОм
КОм
Найдем добротность колебательного контура:
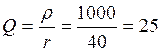
Найдем резонансное сопротивление колебательного контура:
![]() Ом
Ом
Найдем сопротивление транзистора:
![]() Ом
Ом
Напряжение на выходе НЭ:
![]() В
В
Амплитуда рабочей гармоники на колебательном контуре:
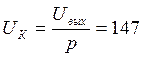 В
В
д) Расчет мощности, поступающей от источника питания:
![]() Вт
Вт
Расчет мощности, выделяемой в нагрузке на рабочей частоте:
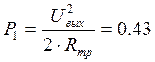 Вт
Вт
Расчет мощности, выделяемой на коллекторе в виде тепла:
![]() Вт
Вт
Расчет полезной мощности на выходе усилителя:
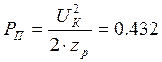 Вт
Вт
Расчет КПД усилителя:
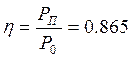
10.4.2. Амплитудная модуляция сигналов.
Задание:
На
вход схемы подается напряжение ![]() , В. На выходе
модулятора необходимо получить АМ сигнал
, В. На выходе
модулятора необходимо получить АМ сигнал ![]() , В.
, В.
Нелинейные искажения при модуляции не должны превышать 10 % (KГ = 0.1), а линейные (частотные) – 30 %. Под частотными искажениями будем понимать изменение коэффициента модуляции M при изменении частоты модуляции от 0 до W.
Исходные данные:
ВАХ НЭ:
u, В |
-2.5 |
-2 |
-1.5 |
-1 |
-0.75 |
-0.5 |
-0.25 |
0 |
|
i, мА |
0 |
0.15 |
0.4 |
1 |
1.5 |
2.25 |
3 |
4 |
|
Um, В |
Uвых, В |
M |
w0, рад/с |
W, рад/с |
r, Ом |
|
0.5 |
5 |
0.25 |
|
200*103 |
8 |
Требуется:
а) построить ВАХ заданного НЭ, в качестве аппроксимирующей функции использовать степенной полином, рассчитать коэффициенты аппроксимирующей функции, построить эту функцию на одном графике с ВАХ;
б) рассчитать и построить статическую модуляционную характеристику;
в) по статической модуляционной характеристике выбрать смещение U0, максимальную амплитуду UW модулирующего сигнала и наибольший коэффициент модуляции Mi тока при неискаженной модуляции;
г) изобразить на одном рисунке ВАХ НЭ, входное напряжение и ток НЭ, используя три координатные плоскости;
д) рассчитать и построить спектр тока на выходе НЭ; при этом входной сигнал не содержит модулирующее напряжение;
е) определить и обосновать параметры контура L, C и r, обеспечивающие допустимые линейные искажения (<30 %, т.е. при D = Mi / M >70 %). Рассчитать фазовый сдвиг j;
ж) выбрать коэффициент включения контура, обеспечивающий требуемую амплитуду Uвых выходного АМ-сигнала. Влиянием НЭ на контур можно пренебречь.
Напряжение питания Eп = 24 В.
а) ВАХ заданного НЭ:
|
|
рис.4. ВАХ НЭ
Определим коэффициенты аппроксимирующей функции:
При
u = -2 В ![]() А
А
При
u = -1 В ![]() А
А
При
u = 0 В ![]() А
А
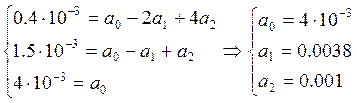
Получаем аппроксимирующую функцию:
![]()
Построим эту функцию на одном графике с ВАХ НЭ:
|
|
рис.5. Аппроксимирующая функция и ВАХ НЭ.
Аппроксимирующая функция обозначена сплошной линией
б) Статическая модуляционная характеристика:
Подставим в уравнение аппроксимирующей функции уравнение входного сигнала:
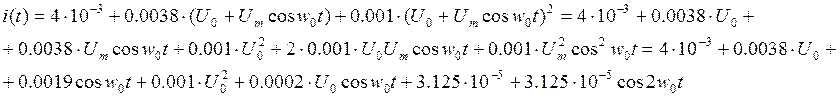
Запишем модуляционную характеристику, т.е. зависимость первой гармоники тока от напряжения смещения:
![]()
|
|
рис.6. Модуляционная характеристика.
Линейная модуляционная характеристика свидетельствует о неискаженной амплитудной модуляции.
в) По статической модуляционной характеристике выбираем напряжение смещения:
U0 = 3 В
U0min = 2 В I1min = 0.0023 А
U0max = 4 В I1max = 0.0027 А
Определим максимальную амплитуду модулирующего сигнала:
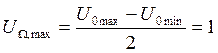 В
В
Определим наибольший коэффициент модуляции тока при неискаженной модуляции:
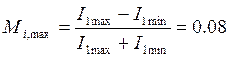
г) ВАХ НЭ, входное напряжение и ток НЭ:
|
|
|
|
рис.7. ВАХ НЭ, входное напряжение и ток НЭ.
д) спектр тока на выходе НЭ:
Подставим в уравнение аппроксимирующей функции уравнение входного сигнала:
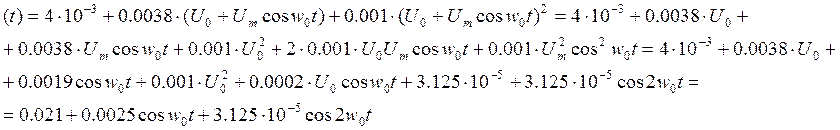 Получим коэффициенты гармоник:
Получим коэффициенты гармоник:
Y0 = 0.021 А
Y1 = ![]() А
А
Y2 = ![]() А
А
|
|
рис.8. Спектр тока на выходе НЭ.
е) Определение параметров контура и расчет фазового сдвига:
Линейные искажения тем меньше, чем меньше добротность, т.е. шире полоса пропускания контура. Исходя из этого условия получим:
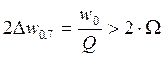
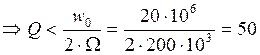
Выбираем добротность: Q = 40
Определим емкость и индуктивность колебательного контура:
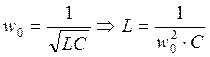
Удельное
сопротивление: 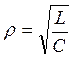
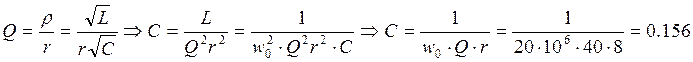 нФ
нФ
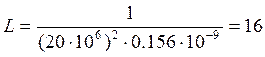 мкГн
мкГн
![]() Ом
Ом
Найдем
обобщенную расстройку: 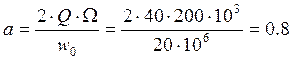
Рассчитаем
фазовый сдвиг: ![]()
ж) Рассчитаем коэффициент включения контура:
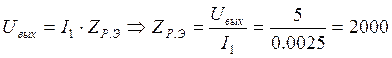 Ом
Ом
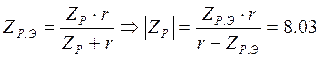 Ом
Ом
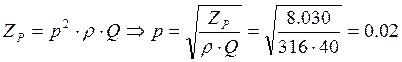
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.