Наука изощряет ум;
Ученье вострит память.
Козьма Прутков
 глава
15
глава
15
ЭЛЕМЕНТЫ СИНТЕЗА ЛИНЕЙНЫХ СТАЦИОНАРНЫХ ЦЕПЕЙ
15.1. Изучаемые вопросы
Синтез аналоговых двухполюсников [2, 13.1, 13.2]. Синтез стационарных четырехполюсников по заданной АЧХ. Фильтры Баттерворта и Чебышева [2, 13.3¼13.5; 1, 15.1, 15.4¼15.8; 24, 2.11, 2.01¼4.06, 7.07, 8.04, 8.14].
Указания. При изучении вопросов необходимо четко уяснить неоднозначность решения задачи синтеза двухполюсников и конкретные пути решения задачи по Фостеру и Кауэру, а также приобрести умение определить возможность реализации той или иной функции входного сопротивления двухполюсника. При синтезе электрических фильтров на основе фильтров-прототипов важно понимать преимущества и недостатки аппроксимации характеристик затухания по Чебышеву и Баттерворту. Необходимо уметь быстро с помощью формул частотных преобразований рассчитывать параметры элементов любых типов фильтров (ФНЧ, ФВЧ, ППФ).
15.2. Краткие теоретические сведения
В теории цепей принято говорить о структурном и параметрическом синтезе. Главной задачей структурного синтеза является выбор структуры (топологии) цепи, удовлетворяющей наперед заданным свойствам. При параметрическом синтезе определяются лишь параметры и тип элементов цепи, структура которой известна. Далее речь пойдет только о параметрическом синтезе.
В качестве исходного при синтезе двухполюсников обычно используют входное сопротивление
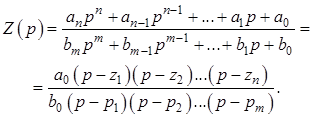
Если задана функция ![]() , то она может быть
реализована пассивной цепью при выполнении следующих условий: 1) все коэффициенты
многочленов числителя и знаменателя вещественны и положительны; 2) все нули и
полюсы находятся либо в левой полуплоскости, либо на мнимой оси, причем полюсы
и нули на мнимой оси простые; данные точки всегда либо вещественны, либо образуют
комплексно-сопряженные пары; 3) высшие и низшие степени многочленов числителя и
знаменателя отличаются не более чем на единицу. Следует отметить также, что
процедура синтеза не является однозначной, т. е. одну и ту же входную функцию
можно реализовать несколькими способами.
, то она может быть
реализована пассивной цепью при выполнении следующих условий: 1) все коэффициенты
многочленов числителя и знаменателя вещественны и положительны; 2) все нули и
полюсы находятся либо в левой полуплоскости, либо на мнимой оси, причем полюсы
и нули на мнимой оси простые; данные точки всегда либо вещественны, либо образуют
комплексно-сопряженные пары; 3) высшие и низшие степени многочленов числителя и
знаменателя отличаются не более чем на единицу. Следует отметить также, что
процедура синтеза не является однозначной, т. е. одну и ту же входную функцию
можно реализовать несколькими способами.
В качестве исходных структур синтезируемых двухполюсников обычно используют цепи Фостера, представляющие собой последовательное либо параллельное соединение относительно входных зажимов соответственно нескольких комплексных сопротивлений и проводимостей, а также лестничных цепей Кауэра [2].
Метод синтеза двухполюсников основан на том,
что заданная входная функция ![]() или
или ![]() подвергается ряду последовательных
упрощений. При этом на каждом этапе выделяется выражение, которому ставят в
соответствие физический элемент синтезируемой
цепи. Если все компоненты выбранной структуры идентифицированы с физическими
элементами, то задача синтеза решена.
подвергается ряду последовательных
упрощений. При этом на каждом этапе выделяется выражение, которому ставят в
соответствие физический элемент синтезируемой
цепи. Если все компоненты выбранной структуры идентифицированы с физическими
элементами, то задача синтеза решена.
Синтез четырехполюсников базируется на теории фильтров-прототипов нижних частот [2]. Возможные варианты прототипа ФНЧ показаны на рис. 15.1.
При расчете может быть использована любая из
схем, так как их характеристики идентичны. Обозначения на рис. 15.1 имеют
следующий смысл: ![]() – индуктивность
– индуктивность ![]() последовательной катушки или емкость
последовательной катушки или емкость ![]() параллельного конденсатора;
параллельного конденсатора; ![]() – сопротивление генератора
– сопротивление генератора ![]() , если
, если ![]() , или
проводимость генератора
, или
проводимость генератора ![]() , если
, если ![]() ;
; ![]() –
сопротивление нагрузки
–
сопротивление нагрузки ![]() , если
, если ![]() или
проводимость нагрузки
или
проводимость нагрузки ![]() , если
, если ![]() .
.
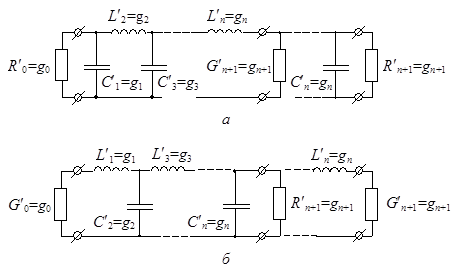
Рис. 15.1
Величины элементов прототипов нормируют так, чтобы ![]() и частота среза
и частота среза ![]() .
Переход от нормированных фильтров-прототипов к другому уровню сопротивлений и
частот осуществляется с помощью следующих преобразований элементов цепи:
.
Переход от нормированных фильтров-прототипов к другому уровню сопротивлений и
частот осуществляется с помощью следующих преобразований элементов цепи:
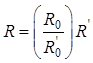 или
или 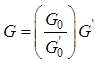 ;
;
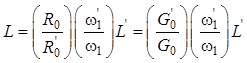 ;
;
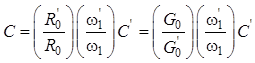 .
.
Величины со штрихами относятся к нормированному прототипу, а без штриха – к преобразованной цепи. Исходной величиной при синтезе является рабочее затухание мощности, выраженное в децибелах:
![]() , дБ,
, дБ,
![]() – максимальная мощность генератора с
внутренним сопротивлением
– максимальная мощность генератора с
внутренним сопротивлением ![]() и эдс
и эдс ![]() ,
, ![]() – выходная мощность в нагрузке.
– выходная мощность в нагрузке.
Обычно частотную зависимость ![]() аппроксимируют
максимально плоской (баттервортовской)
характеристикой (рис. 15.2, а)
аппроксимируют
максимально плоской (баттервортовской)
характеристикой (рис. 15.2, а)
![]() , дБ,
, дБ,
где ![]() .
.
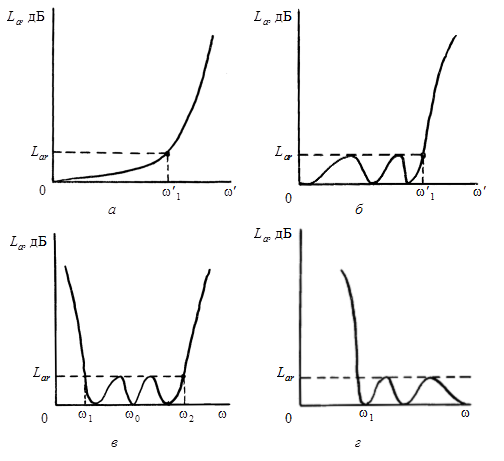
Рис. 15.2
Величину рабочего затухания ![]() ,
соответствующую частоте среза
,
соответствующую частоте среза ![]() , обычно выбирают равной
3 дБ. При этом
, обычно выбирают равной
3 дБ. При этом ![]() . Параметр n
равен числу активных элементов цепи и определяет порядок фильтра.
. Параметр n
равен числу активных элементов цепи и определяет порядок фильтра.
Величины элементов максимально плоских фильтров, нагруженных на
активное сопротивление на входе и выходе и имеющих ![]() дБ,
дБ, ![]() и
и ![]() ,
определяют из выражений
,
определяют из выражений
![]() ;
;
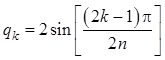 ,
,
![]() .
.
Широкое распространение получила также равнопульсирующая аппроксимация Чебышева (см. рис. 15.2, б)
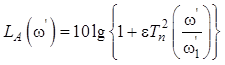 ,
,
где ![]() – полином Чебышева n-го порядка для
– полином Чебышева n-го порядка для ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
т. д.,
и
т. д., ![]() для
для ![]() ;
; ![]() .
.
Полиномы n-го порядка могут быть найдены с помощью рекуррентного соотношения. Основное преимущество чебышевских фильтров по сравнению с максимально плоскими (Баттерворта) – меньшее число элементов, требующееся для обеспечения одинакового затухания на заданной частоте вне полосы пропускания.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.