Для чебышевских фильтров, нагруженных с двух сторон и имеющих характеристики
вида рис. 15.2, б при условии, что ![]() и
и ![]() , а
, а ![]() задано
в децибелах, величины элементов могут быть рассчитаны следующим образом.
Сначала определяются вспомогательные параметры по формулам:
задано
в децибелах, величины элементов могут быть рассчитаны следующим образом.
Сначала определяются вспомогательные параметры по формулам:
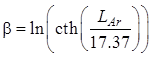 ;
; ![]() ;
;
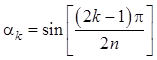 ,
, ![]() ,
,
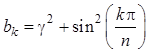 ,
, ![]() ,
,
затем находят величины элементов
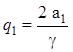 ;
;
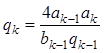 ,
, ![]() ;
;
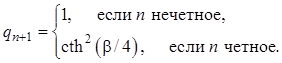
С помощью прототипа ФНЧ можно рассчитать полоснопропускающие фильтры (ППФ), структуры которых показаны на рис. 15.3.
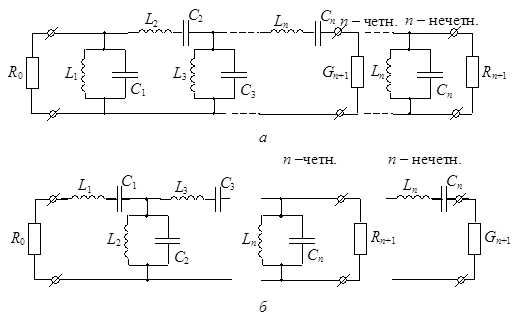
Рис. 15.3
Переход от структур прототипов ФНЧ рис. 15.1, а, б к соответствующим ППФ рис. 15.3, а, б выполняют с помощью частотного преобразования
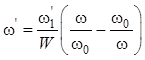 .
.
Полосу пропускания и ее среднюю частоту определяют из выражений
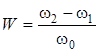 ;
; ![]() .
.
Параметры последовательных и параллельных резонаторов рассчитывают по формулам
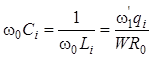 – для параллельных резонаторов;
– для параллельных резонаторов;
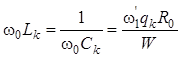 – для последовательных резонаторов.
– для последовательных резонаторов.
В этих выражениях ![]() – значения параметров
элементов прототипа, а частоты
– значения параметров
элементов прототипа, а частоты ![]() ,
, ![]() ,
, ![]() показаны
на характеристике ППФ (см. рис. 15.2, в).
показаны
на характеристике ППФ (см. рис. 15.2, в).
Переход от прототипа ФНЧ к структуре фильтра верхних частот (ФВЧ) (рис. 15.4) происходит с помощью частотного преобразования
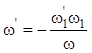 ,
,
здесь ![]() – частота среза (см.
рис. 15.2, г).
– частота среза (см.
рис. 15.2, г).
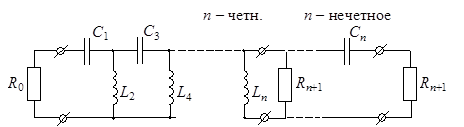
Рис. 15.4
При этом расчет параметров элементов ФВЧ производится по формулам:
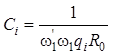 ;
;
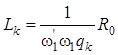 ;
;
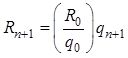 .
.
15.3. Задачи
15.3.1. Синтез двухполюсников
1. Осуществите реализацию двухполюсника по Фостеру в виде последовательного соединения элементов по заданной функции входного сопротивления
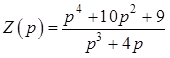 .
.
2. Реализуйте функцию ![]() предыдущей задачи по второй
форме Фостера в виде параллельного соединения проводимостей.
предыдущей задачи по второй
форме Фостера в виде параллельного соединения проводимостей.
3. Получите различные варианты реализации по Кауэру двухполюсника, обладающего входным сопротивлением задачи 1.
4. Реализуйте в виде лестничной цепи Кауэра двухполюсник с входным сопротивлением
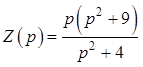 .
.
5. Определите, может ли данное выражение быть функцией входного сопротивления некоторой электрической цепи:
а) 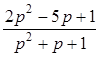 ; б)
; б)
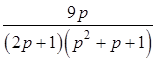 ;
;
в) 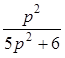 ; г)
; г)
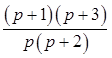 ;
;
д) 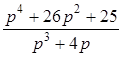 ; е)
; е)
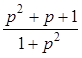 ;
;
ж) 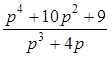 .
.
15.3.2. Синтез четырехполюсников
6. Рассчитайте параметры элементов ФНЧ с максимально плоской характеристикой
затухания, с числом элементов цепи ![]() и
и
частотой среза ![]() рад/с и внутренним
сопротивлением генератора
рад/с и внутренним
сопротивлением генератора ![]() Ом.
Ом.
7. Определите величину затухания ФНЧ (задача 6) на частоте ![]() Гц.
Гц.
8. Определите порядок ФНЧ с плоской характеристикой и частотой среза
![]() рад/с, имеющего затухание не менее 30 дБ на
частоте
рад/с, имеющего затухание не менее 30 дБ на
частоте ![]() рад/с.
рад/с.
9. Докажите, что при одинаковых исходных данных фильтры с чебышевской характеристикой имеют большее затухание за полосой пропускания по сравнению с фильтрами, имеющими плоскую характеристику затухания.
10. Сколько элементовов должен
иметь ФВЧ с чебышевской характеристикой затухания ![]() дБ и
частотой среза
дБ и
частотой среза ![]() рад/с, чтобы обеспечить
затухание
рад/с, чтобы обеспечить
затухание ![]() дБ на частоте
дБ на частоте ![]() рад/с?
рад/с?
11. Сколько резонаторов должен содержать ППФ с максимально плоской
характеристикой затухания, ![]() рад/с,
рад/с, ![]() рад/с, чтобы обеспечить затухание на
частоте
рад/с, чтобы обеспечить затухание на
частоте ![]() рад/с не менее 20 дБ?
рад/с не менее 20 дБ?
12. Чему равна мощность в нагрузке фильтра, если амплитуда эдс генератора на входе ![]() В, внутреннее сопротивление генератора
В, внутреннее сопротивление генератора ![]() Ом, а затухание фильтра
Ом, а затухание фильтра ![]() дБ?
дБ?
15.4. Контрольное задание. Синтез четырехполюсника
По исходным данным, приведенным в табл. 15.1 и 15.2, произвести синтез четырехполюсника (фильтра) на основе фильтра-прототипа НЧ. Осуществить расчет параметров фильтра.
Таблица 15.1
|
Номер варианта |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Тип фильтра |
ФНЧ |
ФНЧ |
ФВЧ |
ФВЧ |
ФВЧ |
ППФ |
ППФ |
ППФ |
ППФ |
ППФ |
Таблица 15.2
|
Номер подварианта |
Исходные данные фильтра |
|||||
|
|
|
|
|
|
Аппроксимация |
|
|
0 |
4 |
0,1 |
10 |
12,5 |
50 |
Чебышева |
|
1 |
4 |
0,2 |
20 |
25 |
75 |
Чебышева |
|
2 |
5 |
3.0 |
30 |
35 |
50 |
Баттерворта |
|
3 |
5 |
0,5 |
40 |
45 |
75 |
Чебышева |
|
4 |
6 |
3.0 |
50 |
60 |
75 |
Баттерворта |
|
5 |
6 |
1,0 |
60 |
70 |
50 |
Чебышева |
|
6 |
7 |
3.0 |
80 |
100 |
50 |
Баттерворта |
|
7 |
7 |
1,0 |
100 |
120 |
75 |
Чебышева |
|
8 |
8 |
3.0 |
150 |
200 |
50 |
Баттерворта |
|
9 |
8 |
2.0 |
200 |
250 |
75 |
Чебышева |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.