Расчет переходного процесса в RLC-цепи методом Рунге-Кутта, страница 8

Таблицы расчетов представлены в «Приложении». Номера таблиц 2-7.
Построение графиков в Excel

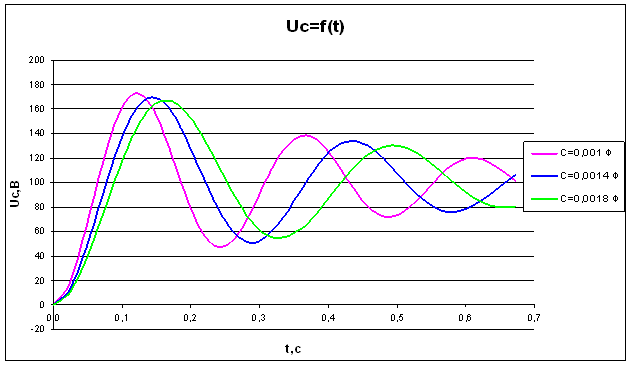
Рис.2 Зависимость напряжения от времени на конденсаторе при R=7 Ом

Согласно физическим законам напряжение установившегося режима на конденсаторе равно ЭДС источника (100 В) (Рис.2 и Рис.3). Напряжение на конденсаторе тем быстрее достигает установившегося режима, чем меньше значение индуктивности и больше сопротивление резистора. Полученная зависимость напряжения на конденсаторе от времени полностью удовлетворяет законам теории основ электротехники.

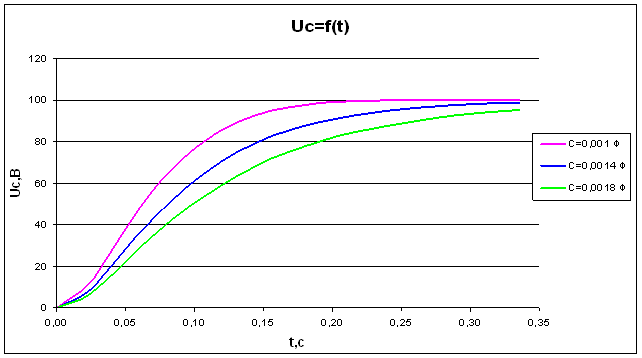 Рис.3 Зависимость напряжения от времени на конденсаторе при R=70 Ом

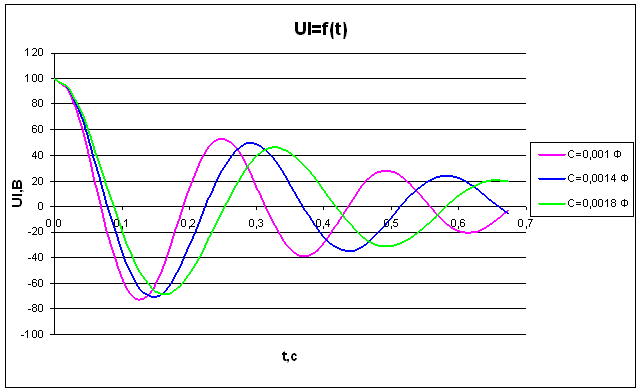 Рис.4 Зависимость напряжения от времени на индуктивности при R=7 Ом

Согласно физическим законам напряжение установившегося режима на элементе индуктивности равно нулю (Рис.4 и Рис.5). Напряжение на элементе индуктивности тем быстрее достигает установившегося  режима, чем меньше значение индуктивности и больше значение сопротивления резистора. Полученная зависимость напряжения на индуктивности от времени полностью удовлетворяет законам теории основ электротехники.

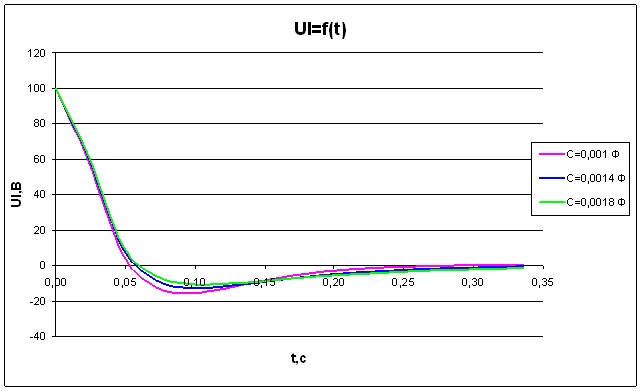 Рис.5 Зависимость напряжения от времени на индуктивности при R=70 Ом

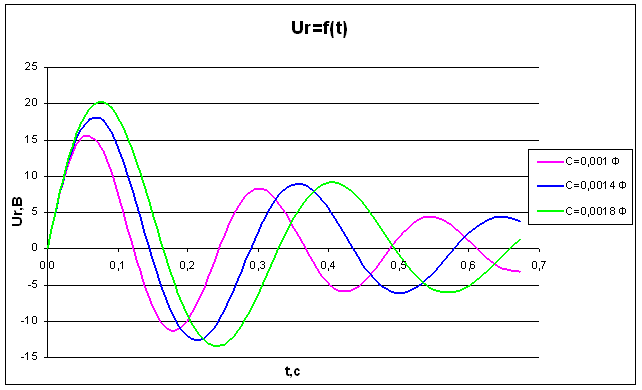 Рис.6 Зависимость напряжения от времени на сопротивлении при R=7 Ом

Согласно физическим законам напряжение установившегося режима резистора равно нулю (Рис.6 и Рис.7). Напряжение резистора тем быстрее достигает установившегося режима, чем меньше значение индуктивности и больше значение сопротивления резистора. Полученная зависимость напряжения резистора от времени полностью удовлетворяет законам теории основ электротехники.

Рис.7 Зависимость напряжения от времени на сопротивлении при R=70 Ом

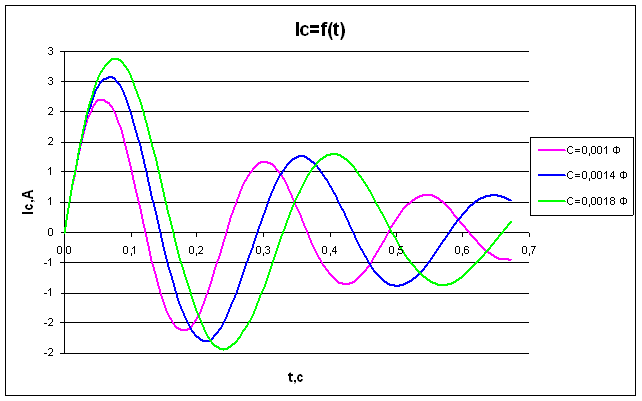 Рис.8 Зависимость силы тока от времени на конденсаторе при R=7 Ом

Согласно физическим законам ток установившегося режима цепи равен нулю (Рис.8 и Рис.9). Ток цепи тем быстрее достигает установившегося режима, чем меньше значение индуктивности и больше сопротивление резистора. Полученная зависимость силы тока от времени полностью удовлетворяет законам теории основ электротехники.

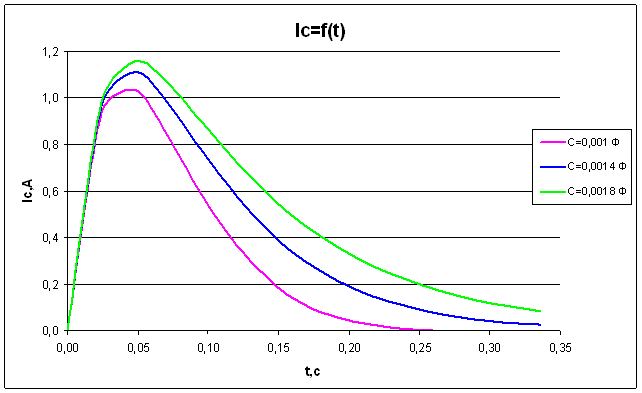
Рис.9 Зависимость силы тока от времени на конденсаторе при R=70 Ом

Расчет переходного процесса на языке QBASIC

Блок-схема

t = t + h Вычисляем Uc, Ur, Ul, I