Расчет переходного процесса в RLC-цепи методом Рунге-Кутта, страница 6

            Величина  называется шагом интегрирования. Шаг интегрирования является переменным, если для различных h величина h_k различна. Если , то говорят, что интегрирование ведется с постоянным шагом. В этом случае  при  k=0,1,2,…, n.

Рассмотрим дифференциальное уравнение первого порядка. Пусть дано дифференциальное уравнение вида

                                                              (6)

            Для заданных значений аргумента x₁, x₂,…, x_n, расположенных в порядке монотонного изменения, требуется вычислить при k=1,2,…,n значения  функции , являющейся решением уравнения (6), если известно начальное значение

                                                                (7)

Решение ищется по рекуррентной формуле

                                                           (8)

Для определения приращения  применяется  метод Рунге-Кутта третьего порядка:

                                                              (9)

Формулы Рунге-Кутта третьего порядка записываются следующим образом:

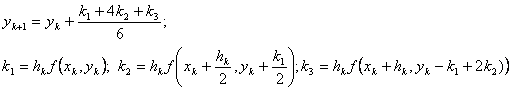                 (10)

Применим метод Рунге-Кутта для дифференциальных уравнений (4):

Значения силы тока и напряжения на конденсаторе будем искать по формуле (8):

  , где di – приращение силы тока.

, где dU_С – приращение напряжения на конденсаторе.

Значения приращения силы тока и напряжения на конденсаторе будем искать по             формуле (9)

При этом                                              (11)

Из формул (10) получим коэффициенты Рунге-Кутта:

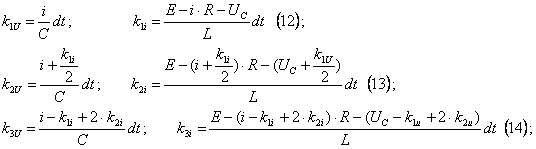
Из законов электротехники известно, что напряжение на индуктивности равно: . А напряжение на сопротивлении равно: .

Значение тока и напряжений в момент времени :

·  Напряжение на конденсаторе равно 0 так как ему необходимо какое-то время для зарядки U_C0= 0 В.

·  Напряжение на катушке индуктивности будет равно напряжению источника из-за ее большого сопротивления и возникновения противо - ЭДС в момент включения ключа U_L0= 100 В.

·  Из формулы  вытекает, что U_R0= 0 В.

·  Из формулы  вытекает, что I₀=0.    

Значение тока и напряжений в установившемся режиме:

·        Напряжение на конденсаторе U_C равно напряжению источника .

·        Напряжение на катушке индуктивности будет U_L равно 0.

·        Из формулы  вытекает, что U_R= 0 В.

·        Из формулы  вытекает, что I=0