Расчет переходного процесса в RLC-цепи методом Рунге-Кутта, страница 10

k2i = (E - (i + k1i / 2) * R(w) - (Uc + k1u / 2)) * h / L

k2u = (i + k1i / 2) * h / C(p)

k3i = (E - (i - k1i + k2i * 2) * R(w) - (Uc - k1u + k2u * 2)) * h / L

k3u = (i - k1i + k2i * 2) * h / C(p)

'точечно строим графики семейств четырех функций

IF w = 1 THEN

 PSET (20 + t * 350, 340 + i * 30), n

 PSET (20 + t * 350, 40 + Uc * .8), n

 PSET (320 + t * 350, 340 + Ur * 4), n

 PSET (320 + t * 350, 125 + Ul * .8), n

ELSE

 PSET (20 + t * 350, 340 + i * 35), n

 PSET (20 + t * 350, 40 + Uc * .99), n

 PSET (320 + t * 350, 340 + Ur * .7), n

 PSET (320 + t * 350, 125 + Ul * 1.55), n

END IF

LOOP UNTIL t > tmax

'закрываем цикл изменения параметра С

n = n + 1

NEXT p

SLEEP

SLEEP

NEXT w

SLEEP

SLEEP

При составлении программы были использованы наиболее удобные операторы языка QBASIC: операторы присваивания, условные операторы, циклы с параметром и с постусловием, операторы ввода-вывода, операторы форматного вывода, графические средства языка QBASIC и др.

Для этого была составлена программа по алгоритму (рис.10). Рассчитанные программой параметры цепи, выведенные в файл TABLES.txt, представлены в Приложении.

Из сравнения таблиц, рассчитанных в табличном редакторе Excel и рассчитанных программой на  языке QBASIC, видно, что значения исследуемых параметров в соответствующие моменты времени совпадают. Это подтверждает правильность решения системы дифференциальных уравнений, описывающей переходной процесс в RLC-цепи

Графики построенные в QBASIC

Графики, построенные средствами языка QBASIC,  идентичны построенным средствами табличного редактора Excel. Анализ зависимостей напряжений и тока в цепи, проведенный для графиков, построенных по рассчитанным в Excel’е данным, справедлив и для зависимостей, рассчитанных по программе на языке QBASIC.

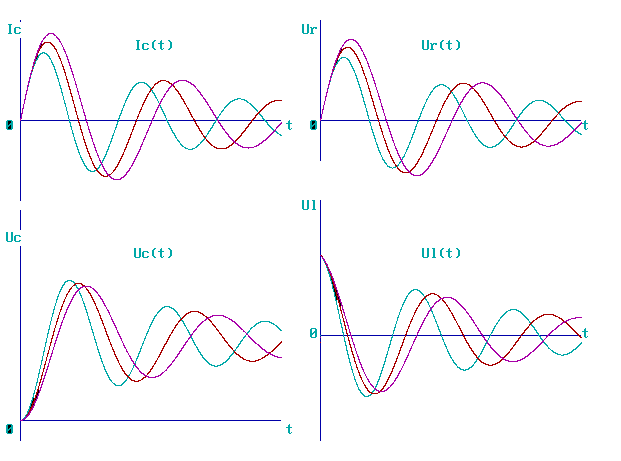
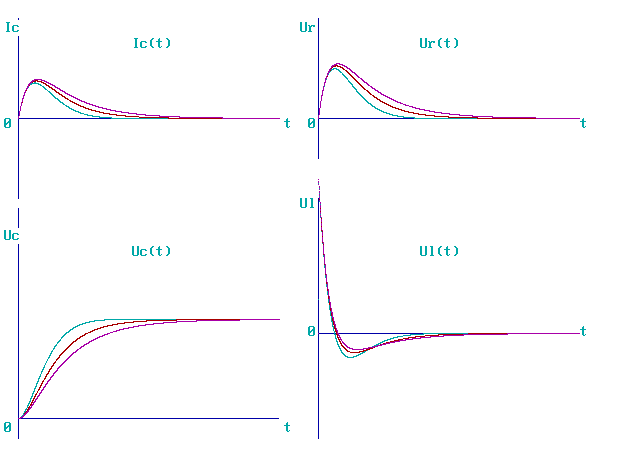
Рис.11

Заключение.

В данной работе с помощью редактора Excel  методом Рунге-Кутта третьего порядка был рассчитан RLC – контур. Необходимо было обеспечить автоматическое изменения результатов расчета при изменении исходных данных, а конкретно - ёмкости. В результате проведенной исследовательской работы по изучению переходных процессов в RLC-цепи были получены зависимости параметров цепи от времени. В соответствии с выбранным методом решения был составлен алгоритм решения системы дифференциальных уравнений и  выбран шаг изменения времени.

В результате решения системы дифференциальных уравнений были получены следующие зависимости параметров RLC-цепи:

Напряжение установившегося режима на конденсаторе равно ЭДС источника (100 В) (Рис.2 и Рис.3). Напряжение на конденсаторе тем быстрее достигает установившегося режима, чем больше сопротивление резистора.

Напряжение установившегося режима на элементе индуктивности равно нулю (Рис.4 и Рис.5). Напряжение на элементе индуктивности тем быстрее достигает установившегося  режима, чем меньше больше значение сопротивления резистора.

Напряжение установившегося режима резистора равно нулю (Рис.6 и Рис.7). Напряжение резистора тем быстрее достигает установившегося режима, чем больше значение его сопротивления.

Ток установившегося режима цепи равен нулю (Рис.8 и Рис.9). Ток цепи тем быстрее достигает установившегося режима, чем  больше сопротивление резистора.

Результаты произведенных расчетов в табличном редакторе Excel совпали с результатами работы программы по расчету переходных процессов в RLC-цепи на языке программирования Qbasic. Кроме этого, были построены графики (в Excel и Qbasic) семейств четырех функций: U_C(t,L), U_L(t,L), U_R(t,L), Iс(t,L), которые также являются идентичными.