Расчет переходного процесса в RLC-цепи методом Рунге-Кутта, страница 5

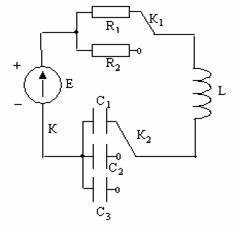
^{Рис.1 Схема электрическая принципиальная последовательной RLC-цепи}

Рассмотрим, как происходит эксперимент, схема которого изображена на Рис.1. При замыкании ключа К в цепи потечет ток, который пройдет через сопротивление R₁ и индуктивность L_, ёмкость С₁ начнет заряжаться; т.е. начнется переходной процесс. В переходном процессе происходят изменения тока и напряжений на конденсаторе, индуктивности и сопротивлении во времени. Ток I и напряжение Ur, изменяясь от 0, достигают сначала своего максимального значения, затем стремятся к 0. Напряжение Uc, изменяясь от 0, стремится к значению Е, а напряжение U_L, изменяясь от своего максимального значения равного Е, стремится к 0. Но при этом все эти изменения представляют собой затухающие синусоидальные колебания. Переходной процесс теоретически закончится, когда I, Ur и U_L будут равны 0, а Uc будет равно E; процесс станет установившимся. Тогда разомкнём ключ К, чтобы конденсатор разрядился. После того как конденсатор полностью разрядится, ключ К опять замкнём, а ключ К2  устанавливаем на С₂, пройдёт тот же процесс, аналогично и для С_3. Когда все три  ёмкости поочередно будут подключены и сняты их показания, цепь замыкаем на R_2. Сопротивление оказывает существенное влияние на скорость затухания колебаний в переходном процессе, т.е. при большом сопротивлении переходной процесс будет протекать быстрее: I, Ur и U_L быстрее достигнут 0, а Uc быстрее достигнет E.В данной курсовой работе должны быть рассчитаны зависимости тока и напряжений на элементах RLC-цепи от времени, построены графики токов и напряжений для различных значений емкости конденсатора.

Выведем расчетные соотношения для RLC – цепи путем применения законов Кирхгофа.

Из первого закона Кирхгоффа для произвольного момента времени получаем:

                                                                                                                     (1)

Из второго закона Кирхгоффа для произвольного момента времени получаем:

(2)  где  - напряжение на индуктивности  в произвольный момент времени,

       - напряжение на активном сопротивлении

С учетом  пояснений формула (2) приобретает следующий вид:

                                                     (3)

Определяем ток на емкостном сопротивлении, а так как соединение контура последовательное, то этот ток будет равен току контура:

                                                            (4)

Преобразуя формулы (3) и (4) получаем систему дифференциальных уравнений первого порядка:

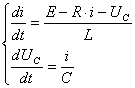                                                                                          (5)

Решение полученной системы дифференциальных уравнений является задачей данной работы, которое будет осуществляться методом Рунге- Кутта третьего порядка.

Решение системы дифференциальных уравнений RLC-цепи

Решение системы дифференциальных уравнений (5) сводится к решению задачи Коши при заданных начальных условиях.

В теории обыкновенных дифференциальных уравнений решение задачи Коши представляет собой некоторое аналитическое выражение , подстановка которого в уравнение (4) обращает последнее в тождество. Решить дифференциальное уравнение (4) численным методом  - это значит, для данной последовательности значений аргумента найти при к=0,1,2,,…,n значения  функции , являющейся аналитическим решением уравнения (4). Таким образом, численное решение дифференциального уравнения (4) сводится к построению для функции , являющейся решением уравнения (4), таблицы её значений, соответствующей заданной последовательности значений аргумента. Аналитическое выражение для функции  при этом, как правило, неизвестно, а в большинстве случаев не может быть найдено в конечном виде.