Профилирование эвольвентных зубьев

Лабораторная работа № 10

Профилирование эвольвентных зубьев

Цель работы: освоение методики нарезания эвольвентных зубчатых колес по методу огибания (обкатки) с различными смещениями инструмента; расчет геометрии эвольвентного зацепления.

Оборудование: прибор для профилирования зубьев ТММ-42, прибор для нарезания бумажных кругов, бумажный круг, остро заточенный карандаш.

Краткие теоретические сведения

Метод огибания при изготовлении эвольвентных зубчатых колес

Зубчатые колеса изготовляют двумя основными способами: копированием и огибанием. Наиболее совершенным по точности профиля и производительности является способ огибания (рис. 10.1). При изготовлении колеса этим способом профили его зубьев образуются как огибающие к семейству положений профилей зубьев производящего колеса (инструмента). Если производящее колесо имеет зубья с эвольвентным профилем (долбяк, рис. 10.1, а), то на заготовке в результате обработки этим способом получают зубья также с эвольвентными профилями. При радиусе колеса, равном бесконечности, инструмент преображается в рейку с прямолинейными профилями зубьев (гребенка, 10.1, б). Такие профили зубьев инструмента просты и технологичны, позволяют изготавливать инструмент с высокой точностью. Наиболее высокопроизводительным методом является нарезание зубчатых колес модульной червячной фрезой (рис. 10.1, в).

Метод огибания позволяет одним и тем же инструментом нарезать колёса с различными числами зубьев и различными формами профиля зубьев, которые определяются не только размерами инструмента, но и его расположением относительно заготовки. Геометрические параметры нарезаемого цилиндрического колеса определяют модулем m и параметрами стандартного исходного контура по  ГОСТ 13755:  углом профиля α = 20º; коэффициентом высоты головки зуба = 1; коэффициентом радиального зазора с* = 0,25; коэффициентом радиуса переходной кривой = 0,38 (рис. 10.2).

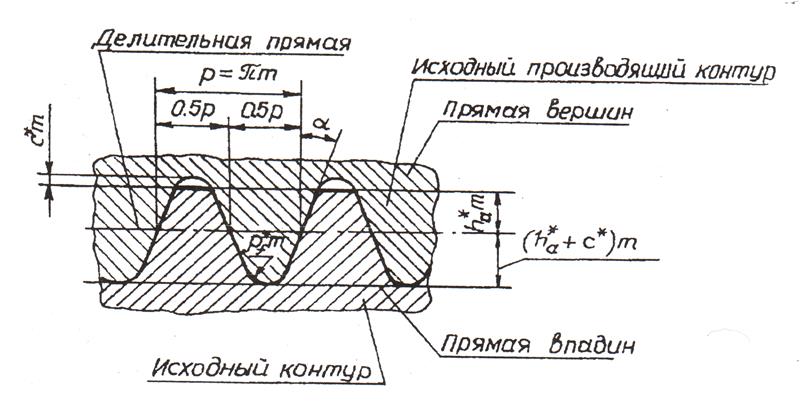
Рис. 10.2. Исходные контуры

Приведенные коэффициенты, помноженные на модуль т, дают геометрические параметры, выраженные этими же символами без звездочек. В зависимости от того, как располагается делительная прямая от инструмента по отношению к делительной окружности нарезаемого колеса, получают нулевые, положительные и отрицательные зубчатые колеса. Смещением ξ = хт называют расстояние от делительной прямой инструмента до делительной окружности колеса, x — коэффициент смещения.

       Нулевое зубчатое колесо нарезают без смещения, то есть xm = 0 и x = 0

(рис. 10.3). В станочном зацеплении начальными являются делительная прямая инструмента и делительная окружность колеса. Так как перекатывание их друг по другу происходит без скольжения,то на делительной окружности нулевого

 колеса толщина зуба равна ширине впадины:

По делительной окружности шаг имеет стандартное значение:

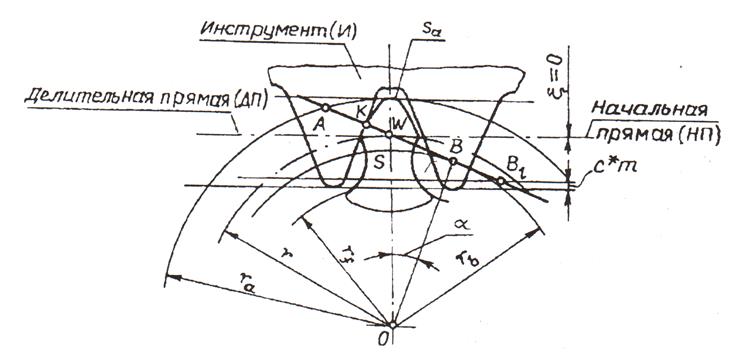
Рис. 10.3. Нарезание нулевого колеса

         Положительное зубчатое колесо с коэффициентом смещения хт > 0 (рис. 10.4) получают при смещении инструмента в радиальном направлении от центра заготовки. На делительной окружности колеса с положительным смещением толщина зуба больше ширины впадины и равна:

Вследствие увеличения делительной толщины зуба ножка становится толще и повышается изгибная прочность зуба.        

         Отрицательное зубчатое колесо с коэффициентом смещения х < 0 (рис. 10.5) получают, если инструмент из нулевого положения переместить к центру нарезаемого колеса. У колеса с отрицательным смещением s < e. Делительную толщину зуба определяют по формуле (10.3), в которую коэффициент смещения x входит со знаком «минус».

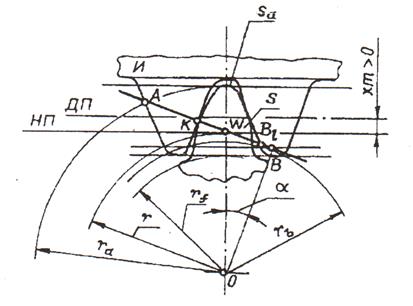
Рис. 10.4. Нарезание положительного колеса

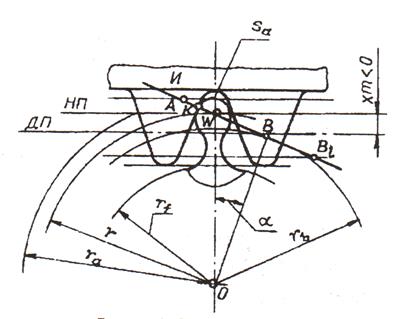
                    Рис. 10.5. Нарезание отрицательного колеса

Подрезание зубьев эвольвентного зубчатого колеса

Активную линию зацепления АВ₁ (рис. 10.3) определяют точками пересечения линии станочного зацепления с окружностью вершин и прямой граничных точек. Изменение величины смещения инструмента изменяет и положение точки В₁ на линии зацепления. Если точка В₁ выйдет за пределы отрезка АВ,определяющего зону контакта сопряженных профилей инструмента и колеса, то произойдет подрезание зуба. При этом инструмент срезает часть главного профиля, уменьшая толщину зуба у основания и снижая его прочность на изгиб. Профили подрезанной части зуба не будут эвольвентными, в результате чего нарушится основная теорема зацепления. Степень подрезания зуба зависит от величины смещения, параметров производящего контура и числа зубьев колеса. Для нулевого колеса минимальное число зубьев, нарезаемых без подрезания, определяют по формуле:

Нарезать без подрезания колесо с числом зубьев z < z_min можно, если дать инструменту положительное смещение, большее или равное минимальному, т.е. х ≥ х_min . Минимальный коэффициент смещения, определяемый из условия неподрезания, равен

В формуле (10.5) число зубьев < 17. Из вышеизложенного можно сделать выводы:

- в нулевом колесе подрезание не произойдет при z ≥ 17;