Профилирование эвольвентных зубьев, страница 5

1)   отрицательного с х₁= 0 и х₂= - 5/m;

2)   нулевого с х₁= 0 и х₂= 0;

3)   положительного с х₁= 0 и х₂ = x_min;

4)   положительного с х₁= 0 и х₂ = +10/m.

По каждому зацеплению студент получает распечатку, из которой параметры колеса выписывает в таблицу формы табл. 10.1.

Таблица 10.1. Оптимизация коэффициента смещения при x₁ = 0

          Образец распечатки параметров эвольвентного зубчатого зацепления с

m  = 10 мм,  z₁ = 12,  z₂ = 12,  х₁ = 0 и  х₂  = 0,3 приведен на рис. 10.9.

Рис. 10.9. Распечатка компьютерных данных положительного зацепления

           По данным табл. 10.1 необходимо построить графики зависимости делительной толщины зубьев колеса s₂, толщины зубьев по окружности вершин колеса s_a2, угла зацепления α_w и коэффициента перекрытия ε_α от коэффициента смещения колеса х₂. По каждой кривой сделать выводы. Кривую s_a2 =  s_a2 (x₂) дополнить горизонтальной прямой  [s_a]_.. = 0,25m и сделать заключение о максимальной величине смещения по условию заострения зубьев. Образец графиков s_a2 =  s_a2 (x₂) приведен на рис. 10.10.

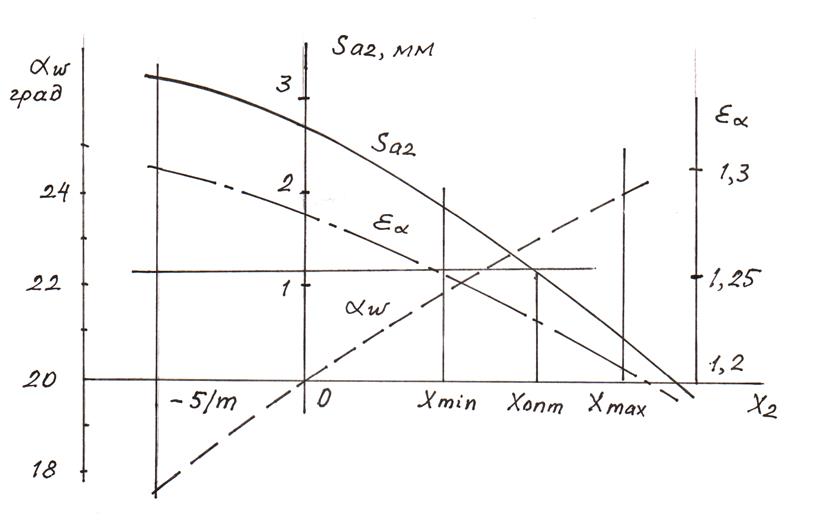
Рис. 10.10. Зависимости характеристик зацепления от коэффициента смещения

Вопросы к защите работы

1. Что такое эвольвента?

2. Какая окружность называется основной? 

3. Что такое шаг зубчатого колеса?

4. Что такое модуль колеса?

5. Какая окружность называется делительной?

6. Каковы основные параметры исходного контура?

7. Каковы достоинства метода обкатки при нарезании зубьев?

8. Какие передачи различают в зависимости от знака смещения?

9.  При каких числах зубьев ножка зуба будет подрезана?

10. Что необходимо сделать для устранения подрезания?

11. Как нарезается положительное зубчатое колесо? 

12. Как и почему меняется профиль зуба при смещении инструмента?

13. Какие задачи решаются выбором оптимальных коэффициентов смещения?

14. Что является признаком повышения контактной прочности?

15. Как влияет смещение на изгибную прочность зубьев?

16. Когда может произойти заострение зуба?

14. Что такое угол зацепления?

15. Что является показателем непрерывности зацепления?  

Практические занятия

В экзаменационные билеты входит ряд задач по эвольвентному зубчатому зацеплению.

А) Вычерчивание эвольвенты окружности.

Построение эвольвенты – один из элементов курсового проекта. Её можно построить по аналитическим данным, см. [2]. На экзамене более компактным будет графическое решение. По модулю m, числу зубьев z и стандартному углу профиля режущего инструмента α = 20º диаметр основной окружности d_b определяют по формуле (10.8). Именно этот параметр определяет форму эвольвенты. Вычерчивают основной диаметр в выбранном студентом масштабе μ_d, мм/мм:

где – отрезок, изображающий величину d_в, мм.

Эвольвенту следует построить по 4  точкам. Первая точка эвольвенты М находится на основной окружности (рис. 10.11).  Для имитации перекатывания угол  МОВ₄ принимают равным 60º и делят его на 4 равные части с интервалом 15º. В точки В₁, В₂, В₃ и В₄  из точки О проводят радиусные прямые ОВ₁, ОВ₂, ОВ₃и ОВ₄ и к ним – перпендикуляры, являющиеся касательными к основной окружности. На касательных откладывают отрезки, равные соответственно МВ₁, 2МВ₁, 3МВ₁ и 4МВ₁. Полученные точки соединяют плавной кривой – эвольвентой. Часть её служит профилем зуба. Эвольвенту ограничивают: