Блокирующие контуры, ограниченные линиями, рассчитанными по уравнениям эвольвенты для различных сочетаний чисел зубьев колёс, позволяют выбрать такие коэффициенты смещения, которые обеспечивают проектирование оптимальной по смещению передачи, у которой зубья не будут подрезаны или заострены, а сама передача будет иметь непрерывное зацепление без заклинивания и с высокими качественными характеристиками. Следует помнить, что
- смещение эффективно для шестерни и малоэффективно для колеса;
- максимально изгибная прочность повышается при максимальном смещении, но при условии отсутствия заострения;
- максимальная контактная прочность обеспечивается при максимальной сумме смещений шестерни и колеса, которая приводит к повышению угла зацепления αw и межосевого расстояния aw.
Пример 10.3. Пользуясь
блокирующим контуром для зубчатой передачи с числами
зубьев z1 и z2, определить смещения
рейки x1 и х2, позволяющие обеспечить
коэффициент перекрытия не менее eа = 1,2 и толщину головок зубьев шестерни не менее ![]() =
0,25m. Оценить выбранную точку по критериям изгибной и контактной
прочности. Рассчитать:
=
0,25m. Оценить выбранную точку по критериям изгибной и контактной
прочности. Рассчитать: ![]() , a, y, aw,
xS, Dy, x1, x2. Исходные
данные: m = 6 мм; z1 = 15; z2 = 36.
, a, y, aw,
xS, Dy, x1, x2. Исходные
данные: m = 6 мм; z1 = 15; z2 = 36.
Решение.
Блокирующий контур с z1/z2 = 15/36 в стандарте (Прил. В) отсутствует. Принимаем контур с ближайшими меньшими z1/z2 = 12/31 (рис. 10.12). На обоих координатных осях откладываем x = xΣ = 1,2 и соединяем полученные точки прямой, на которой находим решение. Точки на контуре необходимо выбирать внутри треугольника, ограниченного смещениями x1 ≥ 0,3; x2 = 0 и линией εα = 1,2. Задача имеет два решения:
а) x1 = 0,3; x2 = 0,9; xΣ = 1,2;
б) x1 = 0,4; x2 = 0,8; xΣ = 1,2.
Оба варианта практически равноценны, они соответствуют максимальной контактной прочности, так как имеют близкую к максимуму сумму смещений xΣ . Рекомендации табл. 10.2 при z1/z2 = 12/34 (x1 = 0,3; x2 = 1,03) имеют близкие значения и также соответствуют максимальной контактной прочности. Принимаем вариант с x1 = 0,4 и x2 = 0,8, так как повышение положительного смещения более эффективно влияет на качественные показатели шестерни, а для колеса смещение малоэффективно. Делительное межосевое расстояние – формула (10.13):
a = 0,5 ∙ 6 ∙ (15 + 36) = 153 мм.
Угол зацепления определяем по инволюте – формула (10.11):
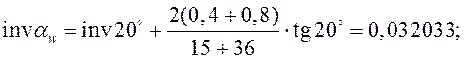
![]() .
.
Межосевое расстояние – формула (10.12):
aw = 153 ∙ cos 20º/cos 25,53º = 159,38 мм.
Коэффициент воспринимаемого смещения – формула (10.14):
y = (159,38 – 153)/6 = 1,06.
Коэффициент уравнительного смещения – формула (10.15):
Δy = 0,4 + 0,8 – 1,06 = 0,14.
Передаточное отношение – формула (10.17):
i12 = - 36/15 = - 2,4.
Пример 10.4. Пользуясь
блокирующим контуром для зубчатой передачи с числами зубьев z1
и z2 и суммарным смещением xS, определить смещения х1 и х2,
позволяющие получить: толщину головок зубьев шестерни не менее ![]() = 0,25m; коэффициент перекрытия не
менее eа =
1,2; отсутствие подрезания. Рассчитать:
= 0,25m; коэффициент перекрытия не
менее eа =
1,2; отсутствие подрезания. Рассчитать: ![]() , d1,
d2, a, df1, df2,
aw. Исходные данные: m = 6 мм; z1 = 13; z2 = 34, коэффициент суммы смещений xΣ = 1,0.
, d1,
d2, a, df1, df2,
aw. Исходные данные: m = 6 мм; z1 = 13; z2 = 34, коэффициент суммы смещений xΣ = 1,0.
Решение.
Блокирующий контур с z1/z2 = 13/34 в стандарте (Прил. В) отсутствует. Принимаем контур с ближайшими меньшими z1/z2 = 12/31 (рис. 10.12). На обоих координатных осях откладываем x = xΣ = 1,0 и соединяем полученные точки прямой, на которой находим решение. Точки на контуре необходимо выбирать внутри треугольника, ограниченного смещениями x1 ≥ 0,3; x2 = 0 и линией εα = 1,2. Задача имеет четыре решения:
а) x1 = 0,3; x2 = 0,7;
б) x1 = 0,4; x2 = 0,6;
в) x1 = 0,5; x2 = 0,5;
г) x1 = 0,6; x2 = 0,4.
Контактная прочность во всех вариантах будет одинаковой, так как она зависит от суммы смещений. Изгибная прочность с увеличением х1 повышается. Принимаем вариант с x1 = 0,6 и x2 = 0,4 из условия максимальной изгибной прочности. Геометрические параметры определяют по формулам, использовавшихся в предыдущих примерах.
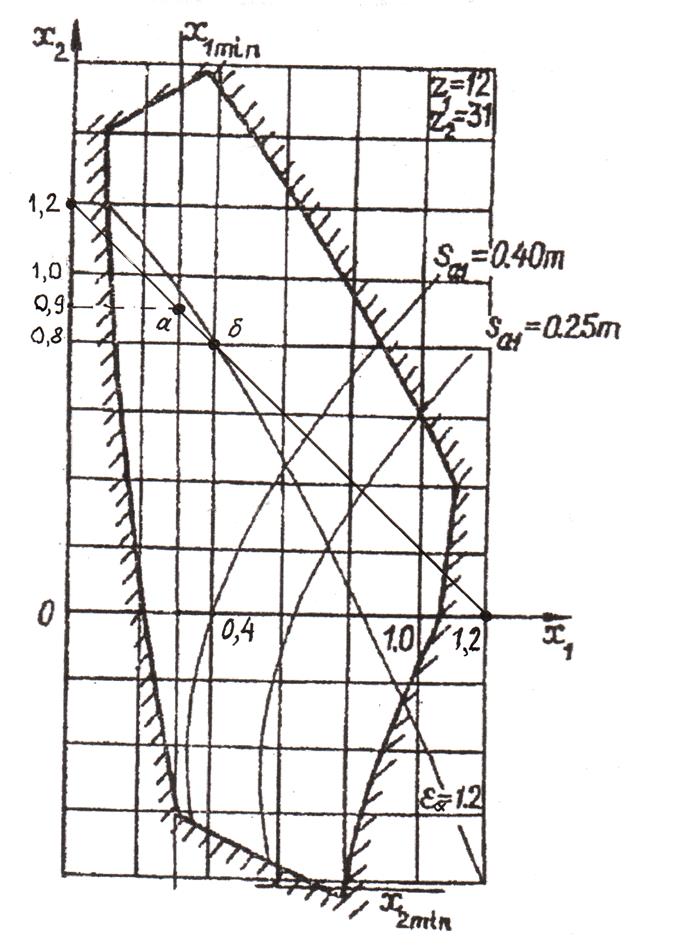
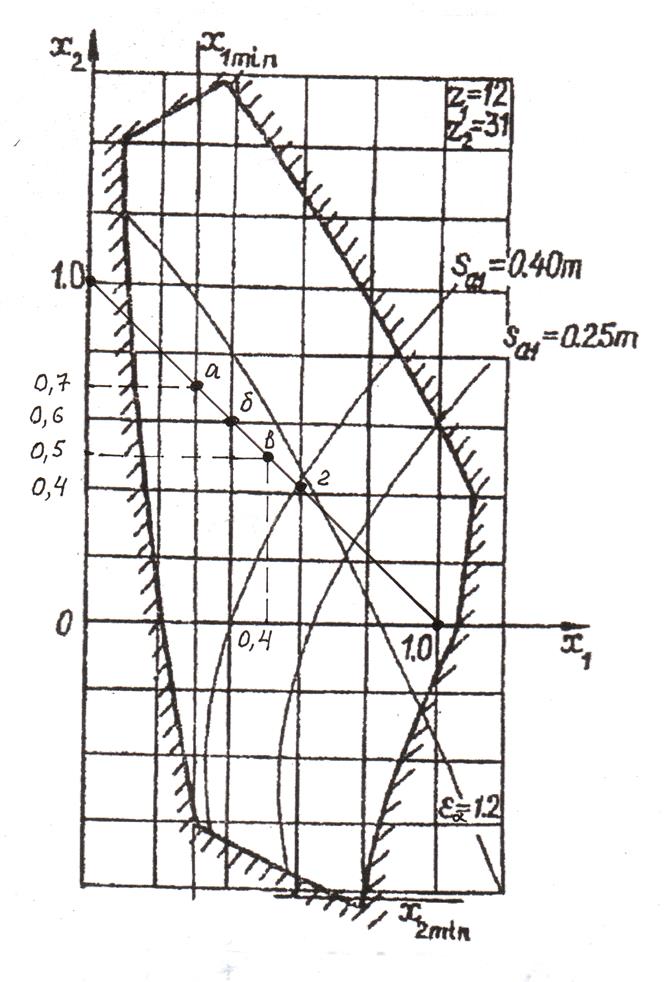
Рис. 10.14. Выбор коэффициентов смещения
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.