Проектирование системы профилактики АТС. Оценка количественных характеристик надёжности на примере автобуса МАЗ-103, страница 9

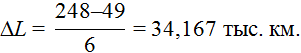
Границы определённых интервалов для наглядности представления сведены в таблицу 6.1.

Таблица 6.1 – Границы интервалов наработки

j

L_{j – 1}

L_{j + 1}

n_j

1

0

83,167

8

2

83,167

117,334

5

3

117,334

151,501

5

Окончание таблицы 6.1

j

L_{j – 1}

L_{j + 1}

n_j

4

151,501

185,688

6

5

185,688

219,835

2

6

219,835

∞

5

Примечание: здесь j – порядковый номер интервала, n_j – количество членов вариационного ряда, находящихся в диапазоне L_{j – 1} ÷ L_{j + 1}.

Теоретические частоты на границах интервалов рассчитываются по формуле

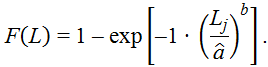
Значения теоретических функций распределения рассчитываются по формуле

Примечание: следует учитывать, что левой границей первого интервала является ноль, а правая граница последнего интервала оканчивается в бесконечности.

Функция распределения отказов для закона Вейбулла-Гнеденко определяется по формуле

ΔF(L_j) = F(L_{j + 1}) – F(L_{j – 1}).

Произведя расчёт по вышеописанным формула можно составить массив исходных данных для определения расчётного критерия согласия Пирсона. Формой представления исходных данных является таблица 6.2.

Таблица 6.2 – Исходные данные для расчёта критерия согласия Пирсона

j

L_{j – 1}

L_{j + 1}

n_j

ΔF(L_j)

1

0

83,167

8

64

0,190

6,066

10,55

2

83,167

117,334

5

25

0,194

6,212

4,025

3

117,334

151,501

5

25

0,209

6,701

3,731

4

151,501

185,688

6

36

0,178

5,680

6,338

5

185,688

219,835

2

4

0,120

3,853

1,038

6

219,835

∞

5

25

0,109

3,488

7,167

Итого

–

–

33

–

1

32

32,849

Критерий согласия Пирсона рассчитывается по формуле

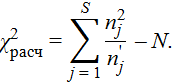
Расчётное значение критерия согласия Пирсона

Поскольку расчётное значение критерия согласия Пирсона не превышает его табличного значения, можно сделать заключение о подтверждении нулевой гипотезы.

7 Оценка вероятности безотказной работы

Вероятность безотказной работы оценивается по формуле Вейбулла-Гнеденко:

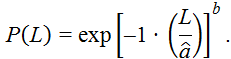
Нижняя доверительная граница

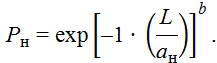
Верхняя доверительная граница

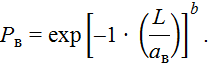
Изменение вероятности безотказной работы фиксируется через каждые 10 тысяч километров наработки, до величины наработки наибольшего элемента вариационного ряда.

Результаты оценки вероятности безотказной работы представлены в таблицах 7.1, 7.2 и 7.3; графическая иллюстрация – на рис. 7.1.

Таблица 7.1 – Показатели вероятности безотказной работы

L

P(L)

L

P(L)

L

P(L)

L

P(L)

L

P(L)

0

1,000

60

0,909

120

0,600

180

0,255

240

0,064

10

0,999

70

0,871

130

0,538

190

0,211

248

0,051

20

0,993

80

0,826

140

0,476

200

0,172

–

–

30

0,982

90

0,775

150

0,416

210

0,138

–

–

40

0,965

100

0,720

160

0,358

220

0,109

–

–

50

0,941

110

0,661

170

0,305

230

0,084

–

–

Таблица 7.2 – Нижние доверительные границы

L

P_н

L

P_н

L

P_н

L

P_н